Application of Gauss Law, Spherical Symmetry, Lecture-3

Lectures on Electricity and Magnetism — new series of lectures – EML – 3.

All articles in this series will be found here. Click on link to left or search for menu “E AND M BASICS” on top.

Application of Gauss Law, Spherical Symmetry, Spherical Shell and Non-conducting Solid Sphere Lecture-3

In our last two lectures we laid a good foundation about the concepts of electric field, lines of force, flux and Gauss Law. They can be found here; EML1 and EML2. In the last one we discussed how to apply Gauss Law to find the electric field if cylindrical or planar symmetries are present in the problem. Today we will discuss how to do the same if spherical symmetry is present. In particular we will discuss two cases

Spherical Shell and
Non-conducting Solid Sphere

+ click to see more about this article

This article belongs to a group of lectures I intend to prepare for their online dissemination — these were delivered in a physical format, beginning with hand written notes that were delivered in a classroom full of students. This series is on Electricity and Magnetism and bears the name sake Electricity and Magnetism Lectures and the number of the lecture will be appended to the end to reflect the same. eg the current lecture will be named EML – 3 . This lecture was delivered to honors students on 2nd Feb 2017.

In the meanwhile if you can’t wait and you need some of these concepts at the earliest, here is a slide-share presentation I had made roughly 5 years ago that consists of “some of the things” an undergrad needs: Electricity and Magnetism slides. There are other slides on different topics at that account of mine on slideshare.net (such as; Introduction to Quantum Mechanics , and these are quite well received by the community for their usefulness).

Spherical Symmetry in a Spherical Shell

A thin spherical shell of radius a has a charge +Q evenly distributed over its surface. Find the electric field both inside and outside the shell.

The charge distribution is spherically symmetric — i.e. it does not depend upon angular parameters (e.g. in a spherical polar coordinate system) but depends only upon position, i.e. radial distance from center of such a system. We can rotate the sphere (shell) about any radial direction and that won’t change the field value or direction.

The surface charge density is total charge over total surface area over which its found, and this is uniform, i.e. does not change from place to place. So it must be given by: σ = Q/(4πa²).

The electric field magnitude E must be radially symmetric (i.e. uniform for a fixed r, in all directions, as we just discussed above) and its direction must be radially outward (charge is positive and it must exert a repulsive force on a positive test charge which must run away from center, for its life)

Lets represent this pictorially in the following diagram.

A thin spherical shell of radius a has a charge +Q distributed uniformly over its surface. It produces a field which is radially symmetric in an outward direction as shown.

The given problem can be discussed in two scenarios, one for the field inside of the shell and the other for the field outside of the shell. Accordingly we discuss case-I and case-II.

Case I: Electric field inside of the spherical shell

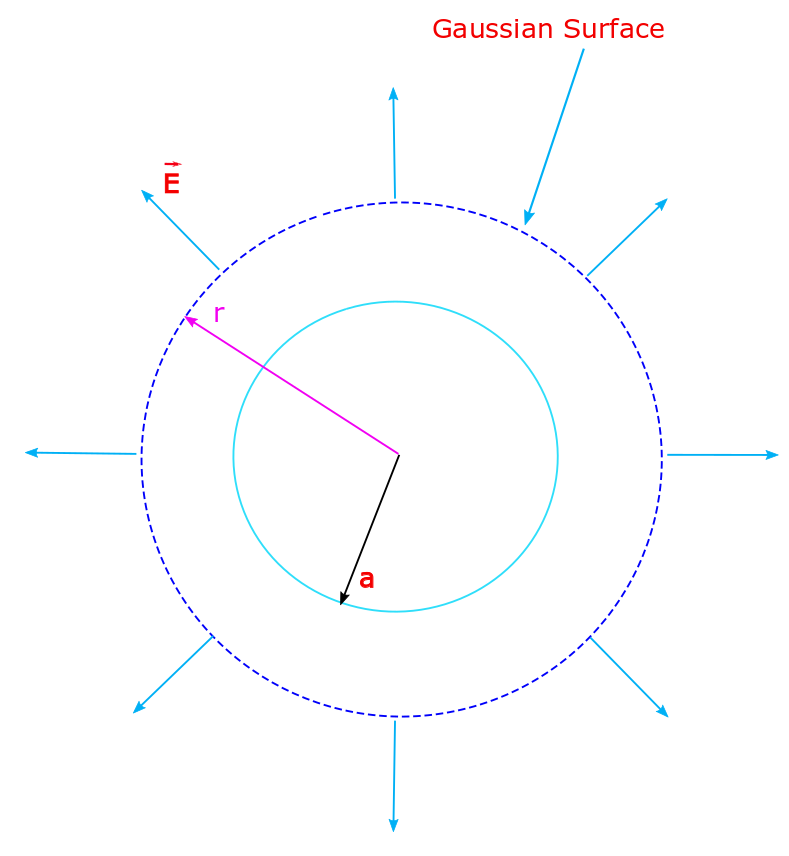
The situation in the first scenario, where we would like to determine the electric field strength magnitude and direction at any point inside of the thin spherical shell is depicted in the following diagram. It shows a suitable Gaussian surface which is a concentric sphere inside of the shell whose surface co-terminates at the points where we would like to determine the field value, i.e. r.

Always remember that a Gaussian surface is one imaginary closed surface that conforms with the symmetry of the situation.
The Gaussian surface encloses a given amount of charge whose electric field is to be determined.

A thin spherical shell of radius a has a charge +Q distributed uniformly over its surface. A Gaussian surface which is a concentric sphere with radius smaller than the radius of the shell will help us determine the field inside of the shell.

For our situation we realize that r ≤ a. The Gaussian surface is a sphere of radius r ≤ a and co-centered (i.e. concentric) with the shell. The charge enclosed is obviously zero, so the net flux is zero as well, from Gauss Law. i.e. q_encl = 0, Φ_E = (q_encl)/ε₀ = 0 ⇒ E = 0 for r ≤ a.

Case II: Electric field outside of the spherical shell

The situation in the second scenario, where we would like to determine the electric field strength magnitude and direction at any point outside of the thin spherical shell is depicted in the following diagram. It shows a suitable Gaussian surface which is a concentric sphere outside of the shell whose surface again co-terminates at the points where we would like to determine the field value, i.e. r.

For our situation we realize that r ≥ a. The Gaussian surface is a sphere of radius r ≥ a and co-centered (i.e. concentric) with the shell. The charge enclosed is obviously q_encl = Q, so the net flux is given by Gauss Law. i.e. $\Phi_E=\iint_S \vec{E}\cdot d\vec{A}=EA=E(4\pi r^2)$ . Thus the electric field strength is given by: $\boxed{E(r)=\frac{Q}{4\pi \epsilon_0}\frac{1}{r^2}=k\frac{Q}{r^2},\,\,\,r\geq a}$ . This expression is same as we would get for all this charge Q to be concentrated at the center.

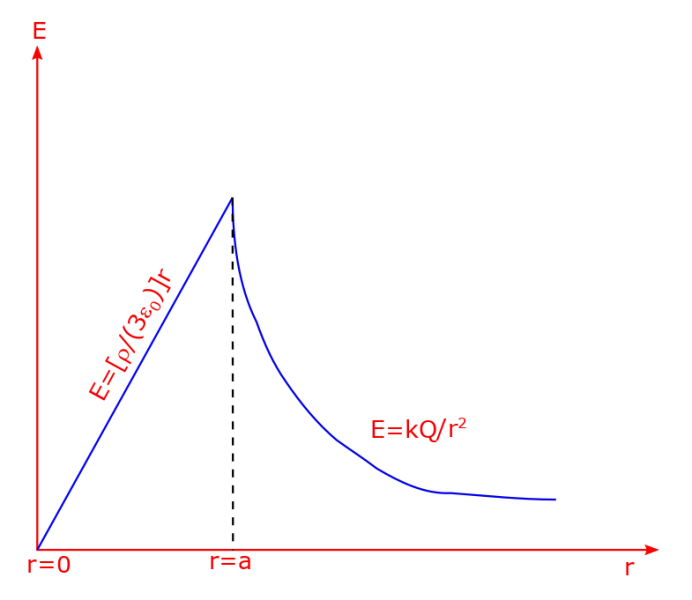
Below is a plot of the electric field strength as a function of radial position r, for all points, i.e. inside as well as outside of the shell.

Plot of the electric field strength for a shell as a function of radial position r, for all points, i.e. inside as well as outside of the shell.

Spherical Symmetry in a Non-Conducting Solid Sphere

An electric charge +Q is uniformly distributed throughout a non-conducting solid sphere of radius a. Determine the electric field everywhere inside and outside of the sphere.

The charge distribution is again spherically symmetric. We can write the volumetric charge density (which is uniform, i.e. same at every point inside of the solid sphere) as ρ = Q/V = Q/[(4/3)πa³).

Electric field is radially symmetric and directed outward (for a positive charge). Field strength E is thus constant on spherical surfaces of radius r, in all directions, like we saw before for spherical symmetry. As before we discuss two scenarios.

Case I: Electric field inside of the solid sphere, r ≤ a

The Gaussian surface is a sphere of radius r, so that r ≤ a.

A non-conducting solid sphere of radius a has a charge +Q distributed uniformly throughout. A Gaussian surface which is a concentric sphere with radius less than the radius of the sphere will help us determine the field inside of the shell.

To calculate flux we use Gauss Law: $\Phi_E=\iint_S \vec{E}\cdot d\vec{A}=EA=E(4\pi r^2)$ . The charge that is enclosed is proportional to the volume of the Gaussian sphere. So, $q_{encl}=\int \rho dV = \rho V = \rho (\frac{4}{3}\pi r^3)=Q\frac{r^3}{a^3}$ . $\Phi_E = \frac{q_{encl}}{\epsilon_0}\implies E(4\pi r^2)=\frac{\rho}{\epsilon_0}\bigg(\frac{4}{3}\pi r^3\bigg)$ . Thus the electric field strength is given by: $\boxed{E(r)=\frac{\rho r}{3\epsilon_0}=\frac{Qr}{4\pi\epsilon_0 a^3}, \,\,\,r\leq a}$ .

Case II: Electric field outside of the solid sphere, r ≥ a

The Gaussian surface is a sphere of radius r, so that r ≥ a. Its shown in the following diagram.

Here the total charge is enclosed within the Gaussian surface. So obviously q_encl = Q. Flux is given by: Φ_E = E(4πr²). From Gauss Law: E(4πr²)=Q/ε₀. Thus the electric field strength is given by: $\boxed{E(r)=\frac{Q}{4 \pi \epsilon_0}\frac{1}{r^2}=k\frac{Q}{r^2}, \,\,\,r\geq a}$ .

This result is same as the result of having all the charge concentrated at the center. The following plot shows the relationship between the field strength at all points as a function of separation from the center of the solid sphere.

Plot of the electric field strength for a non-conducting solid sphere as a function of the radial position r, for all points, i.e. inside as well as outside of the sphere.

Rate this:

Comments

2 responses to “Application of Gauss Law, Spherical Symmetry, Lecture-3”

Conservative Nature of the Electrostatic Field and Electrostatic Potential, Lecture – 4. – M Dash Foundation: C Cube Learning

June 30, 2020

[…] charged rod and an infinitely large non-conducting sheet of uniform charge. In the 3rd one (and EML3) we discussed how to do the same if spherical symmetry is present e.g. in the case of a spherical […]

LikeLike

Laplace And Poisson Equation, Lecture 5, 6, 7 And 8. – M Dash Foundation: C Cube Learning

July 4, 2020

[…] rod and an infinitely large non-conducting sheet of uniform charge. In the 3rd one (and EML3) we discussed how to do the same if spherical symmetry is present e.g. in the case of a spherical […]

LikeLike