If you would like to become a nuclear physicist, what you would like to know about the nucleus first?

Lectures on nuclear physics series. All nuclear physics lecture of this series can be accessed here.

Constituents of the nucleus and their intrinsic properties

Qualitative facts about mass, radii, charge density

This lecture, the first in the series of lectures on nuclear and particle physics as a paper for honors degree class, was delivered on 5th July 2017.

Topics covered in this lecture

A. structure of the nucleus

B. properties of the nucleus

Structure of the nucleus

Every atom consists of a dense positive central core of mass, known as nucleus. Its size is much smaller compared to the size of the atom, but nonetheless it contains almost all of the mass of the atom.

The nucleus is made of only neutrons and protons. — These are collectively known as nucleons.

Nucleons are not the smallest constituents of matter. — In-fact nucleons are made of different combinations of 3 quarks, of which only two of the quarks can be of the same type.

Combinations of 3 quarks which form into a bound state of material system are known as baryons. We will study about baryons in the last part of this lecture series.

Thus baryons are a naturally occurring collective matter, built from 3 quarks, where the 3 quarks interact among each other, but can’t escape this bound state of formation, even under the impact of tremendous force.

This fact is known as asymptotic freedom, such freedom is only a dream for them, and for us. This is possible in principle, when the distance of separation between them can be made infinite, in order to weaken the existing attractive force between them, to zero.

As we just mentioned, above, nucleons, a collective name for neutrons and protons, interact among them in an attractive fashion. The attractive force through which nucleons interact among them, is known as strong force — or strong nuclear force. In-fact strong force is the strongest known fundamental force in nature.

The stability of a nucleus depends upon the net attractive force due to strong force and the net repulsion among protons due to electromagnetic force between the same. — This is much in the same way our financial stability in increased by how much we earn, but decreases by credits, loans, mortgages and unnecessary spending.

Remember that electromagnetic force while much weaker than the strong force is considerably strong enough to destabilize the nucleus. Its the neutrons which provide stability, as much as the protons do.

But due to electric charge of the protons, there is some tussle between different protons to have a tendency to run away from the household chores, and in effect destabilize the nucleus home. Why are some people so angry? They have secondary forces causing a lot of aggression in them.

When a nucleus is unstable, it decays. A particular nucleus decays into other stable nuclei and any other possible list of particles. — Such processes are known as nuclear reactions.

In-fact there is a technical difference between a nuclear decay and a nuclear reaction.

It is that, the nuclear decay refers to spontaneous processes involving the nuclei.

Examples are nuclei releasing radioactive entities such as $\alpha,\, \beta$ particles and gamma rays — gamma rays are universally denoted by the symbol gamma, $\gamma$ a small Greek letter.

But in a nuclear reaction, one has to induce the process, from outside.

One has to instigate the constituents in the nucleus home, to break away or cause instability and produce new particles, one or more old particles break or produce new particles including new nuclei, according to what is possible in terms of laws of nature.

We will study more about them, later in this course.

Nuclear reactions sometimes involve another fundamental force of nature — known as weak force or weak nuclear force. Its strength is quite less even from electromagnetic force.

— Its like your distant cousin, who sometimes appear from nowhere and causes you both exhilaration and embarrassment. The cousin can make or break some of your important relations. Weak force does exactly that.

Now let us shed some light on the very basic properties of the nucleus.

Properties of the nucleus

According to the Rutherford’s experiment a nucleus is tens of thousands of times smaller than the radius of an atom.

According to many modern scattering experiments which use probes such as high energy protons, electrons, neutrons or $\alpha$ particles — which is nothing but the helium nuclei with 4 nucleons, — $_2\,He\,^4$ , — the radius $R$ of a nucleus depends on the total number of nucleons in a nucleus, in the following manner.

$\boxed{R = R_0 \, A^{\frac{1}{3}}}$

where $R_0$ is the experimentally determined constant with a value of 1.2 femto-meter ( short fm ) i.e. $1.2 \times 10^{-15}\,m$ and $A$ is known as nucleon number or mass number.

Mass-number is the nearest whole number to the mass of a given nucleus for which it is being quoted, when expressed in terms of the atomic mass unit — amu or $u = 1.66053878 \times 10 ^{-27}\,kg$ .

Both protons and neutrons are approximately $1\,u$ . All the following masses we have below are rest-masses.

Proton: $m_p = 1.007276\,u = 1.672622\times 10^{-27}\,kg$

Neutron: $m_n = 1.008665\,u = 1.674927\times 10^{-27}\,kg$

Electrons: $m_e = 0.00548580\,u = 9.10938\times 10^{-31}\,kg$

Nuclear density: We can calculate the nuclear density as we know, its mass and its radius. From the above boxed expression we see therefore that the volume of the nucleus $V$ is proportional to the mass or nucleon number $A$ , i.e. the total number of neutrons and protons.

Nuclear volume is $V= \frac{4\pi}{3}R^3$ and $R = R_0 \, A^{\frac{1}{3}}$ .

Thus the nuclear density is independent of total number of neutrons and protons, in other words all nuclei have approximately the same density.

Now let us solve a numerical problem to spruce up what we learned from the above discussion.

Calculating nuclear properties

The most common kind of iron nucleus has mass number $A = 56$ .

Find the radius, approximate mass and the approximate density of the nucleus.

Answer

$R = R_0 \, A^{\frac{1}{3}}=56^{\frac{1}{3}}(1.2\times 10^{-15})\,m=4.6 \times 10^{-15}m= 4.6\, fm$ .

$m\approx (56\,u)\big(1.66\times10^{-27}\,\frac{kg}{u}\big)=9.3\times 10^{-26}\,kg$ .

$V=\frac{4\pi}{3}R^3=\frac{4\pi}{3}(4.6\times10^{-15})^3=4.1\times 10^{-43}\,m^3$ .

$\rho = \frac{m}{V}=\frac{9.3\times 10^{-26}}{4.1\times 10^{-43}}=2.3 \times 10^{17}\, \frac{kg}{m^3}$ .

Atomic number and neutron number: We define atomic number $Z$ as the number of protons in a nucleus. Similarly number of neutrons $N$ in a nucleus is called the neutron number.

Thus the nucleon number or mass number $A$ is now given by: $A = Z + N$ .

When a particular type of nucleus is considered its atomic number ( $Z$ ) and its neutron number ( $N$ ) are fixed. Then such a species is called a nuclide.

Chemical properties of an atom is determined by its electronic structure or configuration which is in turn decided by charge of the nucleus $Z \, e$ .

Isotopes: Isotopes are a set of nuclides with same atomic number ( $Z$ ) but different neutron numbers ( $N$ ). As a consequence isotopes have different ( $A$ ).

Isotopes therefore have the same nuclear charge nut different mass.

The following lists various possible stable isotopes of a bunch of nuclide. We mention only two isotopes for each nuclide.

Note that uranium isotopes are not stable, i.e. they are radioactive, but they are primordial isotopes, the ones that were created before formation of earth and are available in their present form.

You can find out an exhaustive list and categorize them as stable vs unstable, natural vs artificial and mention their relative abundances. Homework is fun.

Here is an image that depicts the special case of oxygen — which has 3 stable isotopes, but the image highlights the idea of isotopes, not the fact about how many there are.

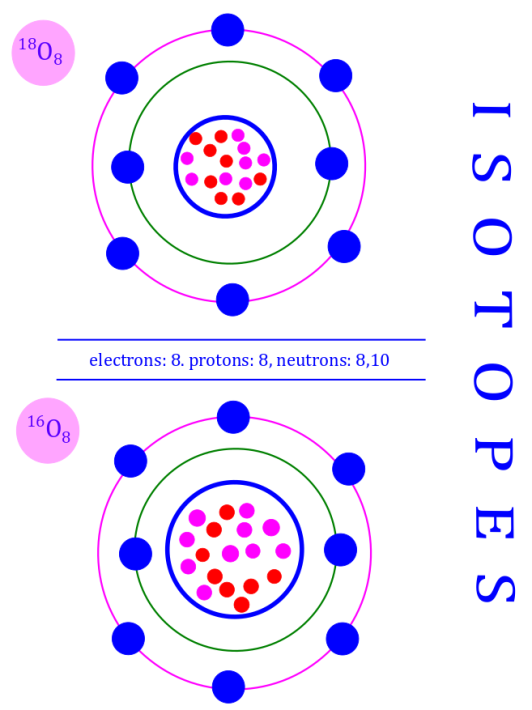
Two stable isotopes of oxygen: this image explains what are isotopes. It describes isotopes by example of oxygen, whose two stable isotopes have different neutron numbers. Photo Credit: mdashf.org — **Two stable isotopes of oxygen**: this image explains what are isotopes. It describes isotopes by example of oxygen, whose two stable isotopes have different neutron numbers. **Photo Credit**: mdashf.org

Hydrogen: 
H-1; ( A = 1, Z = 1, N = 0 ) - Protium
H-2; ( A = 2, Z = 1, N = 1 ) - Deuterium

Lithium: 
Li-6; ( A = 6, Z = 3, N = 3 ) 
Li-7; ( A = 7, Z = 3, N = 4 ) - most abundant

Boron: 
B-10; ( A = 10, Z = 5, N = 5 ) 
B-11; ( A = 11, Z = 5, N = 6 ) - most abundant

Carbon: 
C-12; ( A = 12, Z = 6, N = 6 ) - most abundant
C-13; ( A = 13, Z = 6, N = 7 )

Uranium: 
U-235; ( A = 235, Z = 92, N = 143 )
U-238; ( A = 238, Z = 92, N = 146 )

Rate this:

Mahisapat, Dhenkanal, Odisha 759001, India