Category: classical mechanics
-
Cross and Dot product of vectors.
Someone asked a very interesting question on the role of vectors in Physics. He was curious to know if dot product of vectors is natural but vector product is just syncretism, — that is make shift or unnatural manipulation. Every vector can be resolved into two components. The cosine and sine components (any two vectors…
-
Coriolis Force; an interesting idea
Coriolis Force The article is 5.34 K worded. I have been thinking of writing a basic introduction, on this important physical concept — of, what’s known as a Coriolis force. It is one of the interesting ideas of physics, which does not get as much of a mention perhaps, unless you just happen to know…
-
Solutions to Irodov problems
Problems In General Physics, I.E. Irodov Part-I Physical Fundamentals in Mechanics. Chapter 1.1 Kinematics. 10 interesting problems in elementary mechanics This post intends to provide 40 interesting problems in elementary mechanics from IE Irodov, Problems in general physics that I solved in last couple weeks. Note that another 30 problems (additional 12 at hand) which…
-
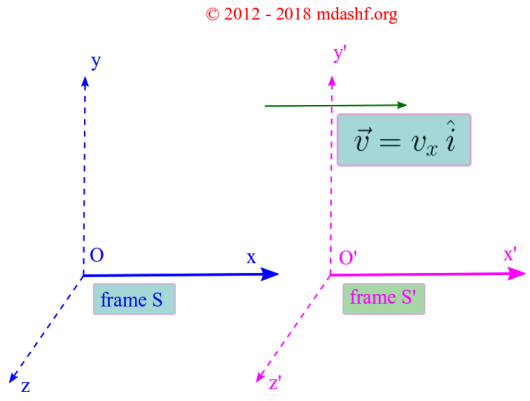
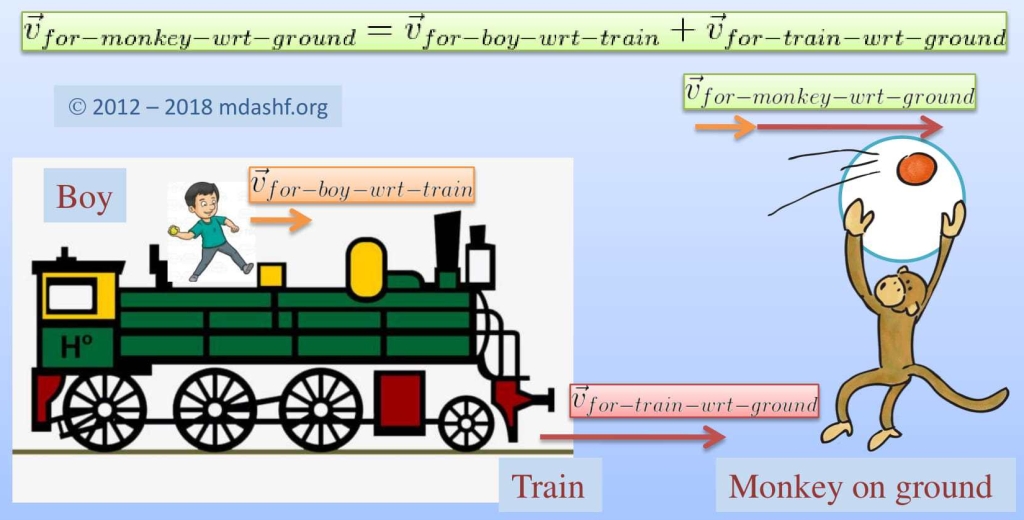
How to add speeds; Galileo and Einstein won’t agree.
How to calculate the speed of anything, when their speed becomes closer to the speed-of-light. This article was originally a comment in the linked article; Why Nothing Moves Faster Than Light. — In order to correct the comment I have made earlier ” unless something is completely mass-less in its rest-frame ” I also add the following. This…
M Dash Foundation: C Cube Learning 