Category: CSIR NET (Physics)
-
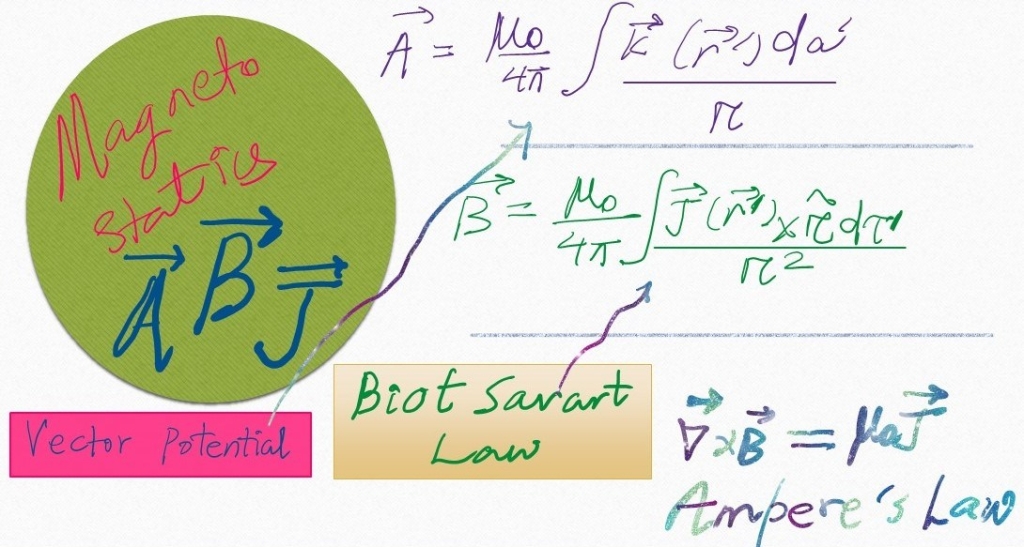
Magnetic vector potential of a rotating uniformly charged shell.
Today we will solve the problem of finding magnetic vector potential of a rotating, uniformly charged spherical shell. We won’t discuss the general idea behind the vector potential (how it follows from Helmholtz theorem, and gauge freedom etc) and how its defined. That will be part of a conceptual lecture and will be available when…
-
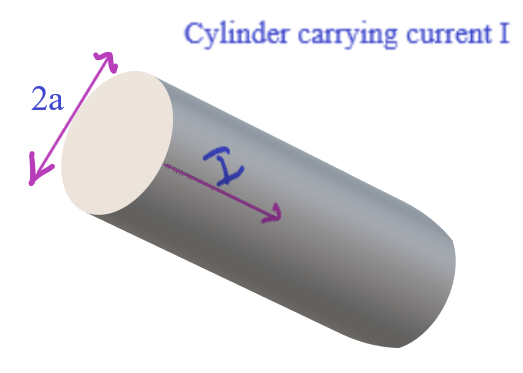
Problem 5.13 Application of Ampere’s Law.
Yesterday we saw an interesting application of the Ampere’s Law (– in magnetostatics and sometimes called Ampere’s circuital law also) for the infinite uniform surface current. Today we will see yet another display of the elegance and efficacy of this law in the following problem. This problem is inherited from Griffith’s text on Electrodynamics (3rd…
-
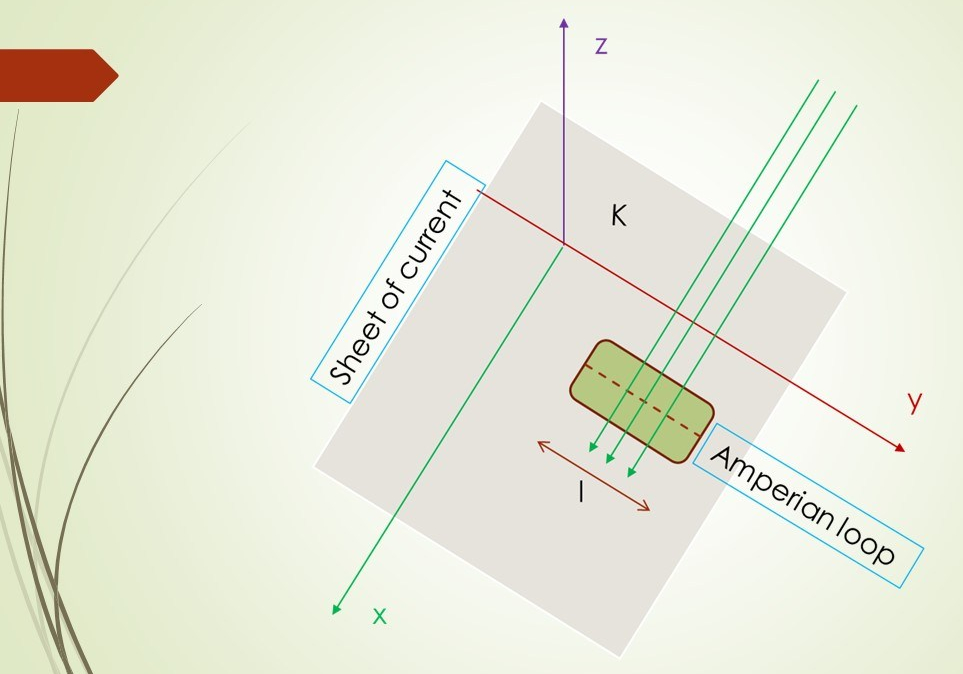
Example 5.7; Application of Ampere’s law.
The following problem is an interesting application of Ampere’s law apart from usual applications found in honors syllabus (eg infinite straight conductor, Solenoid and Torroid). This is to be found the excellent book by Griffith on Electrodynamics. Find the magnetic field of an infinite uniform surface current K (vect) = K i-cap, flowing over the…
-
CSIR NET 2018 December Physical Science Solutions Part-B
The CSIR NET 2018 held on December 16: Indian Assistant Professor and PhD scholarship exam solution, prepared by me. The answers and detailed explanations are available for 18 out of 25 questions of Part-B. The detailed explanations and answers to Part-A is also available, see link below. Please point out any inadvertent errors. (this is…
-
The CSIR NET 2018 December solutions
The article aims to make the best attempt at finding the answers for the recently concluded 2018 CSIR NET. Detailed explanatory answers are available to 19 out of 20 questions in Part A, at the moment. Only physical sciences paper part B and C will be added. CSIR NET 2018 December physical sciences Part A…