Category: Relativity
-
Why light would curve under gravity?
Everyone was thinking in terms of physics (i.e. force). Einstein knew one part of that is maths, pure maths. Force is physics because of mass. But acceleration is geometry, its the shape of your trajectory and its maths. Imagine a pipe which is horizontally fitted across a wall. Now water jet is flowing through it,…
-
Four-vectors and conservation laws in relativity
This lecture was delivered to the final year honors class of 3 year science degree students on 21 November 2017 as part of the Classical Dynamics paper. In this lecture we will discuss some of the important tools of relativistic mechanics. We will discuss the idea of proper-time, 4-velocity, 4-acceleration, 4-momentum, 4-force and related conservation…
-
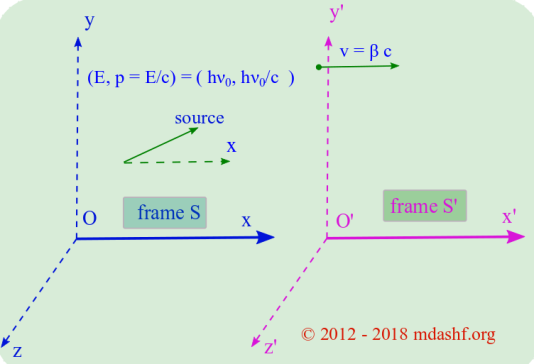
Relativistic Doppler effect
Relativistic Doppler effect. There is an apparent shift in the observed frequency of any electromagnetic wave (light) when there is any relative motion between the source of light and the observer. This can be easily determined by using the 4-vector formulation of theory of relativity. Lets discuss the details of this phenomena under two situations.…
-
Introduction to special theory of relativity.
Special Theory of Relativity: Galilean Transformations,. Newtonian Relativity. This was a lecture delivered to physics-elective class of a 3 year non-physics degree students on 10th April 2017. This is also a good exposition to honors students and anyone at an introductory level of the special theory of relativity, with requisite mathematical background. Let us consider…
-

Gravitational Anomaly
Gravitational Anomaly: (asked by a student for very simple explanation) Basically it means the new laws of physics known as Quantum Mechanics invalidates the sanctity of nature’s principles or laws (that is QM brings exceptions to the validity of the physical laws of nature itself) Let us discuss this in simpler ideas from the basics…