Tag: relativity theory
-
Four-vectors and conservation laws in relativity
This lecture was delivered to the final year honors class of 3 year science degree students on 21 November 2017 as part of the Classical Dynamics paper. In this lecture we will discuss some of the important tools of relativistic mechanics. We will discuss the idea of proper-time, 4-velocity, 4-acceleration, 4-momentum, 4-force and related conservation…
-
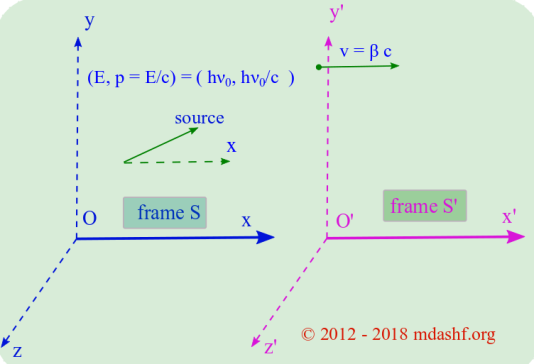
Relativistic Doppler effect
Relativistic Doppler effect. There is an apparent shift in the observed frequency of any electromagnetic wave (light) when there is any relative motion between the source of light and the observer. This can be easily determined by using the 4-vector formulation of theory of relativity. Lets discuss the details of this phenomena under two situations.…
-
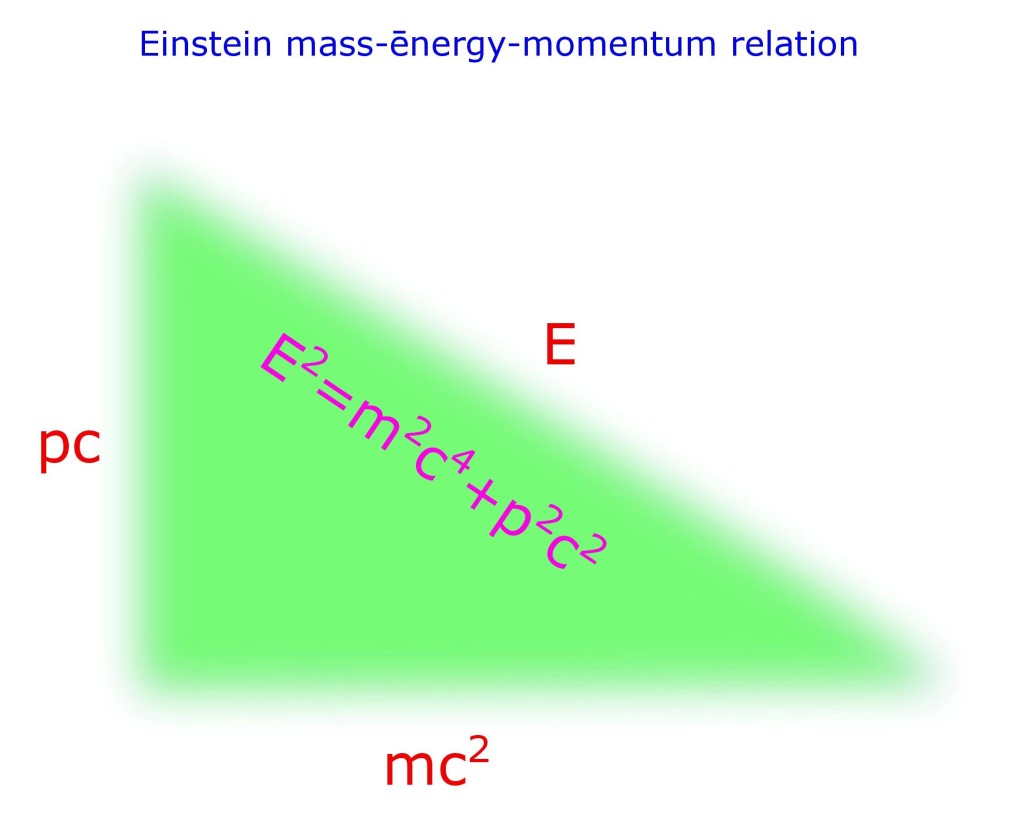
Waves, particles and Einstein !
Waves are something that have no mass and move at the maximum speed, mass m = 0. speed c = 1. So whats their momentum? p = m.v = 0? Right? No. For pure waves; momentum does not come from mass. It comes only from motion. (pure wave; they do not have mass) For matter…
-
What happens when cows move rapidly !
Cows not moving and moving fast. How does this difference impact the image in a modern digital camera? Honestly I haven’t checked it with old day manual camera neither do I remember what impact motion brings into mages taken by such, eg does anyone remember when he/she took a picture of a friend standing in…
M Dash Foundation: C Cube Learning 