Waves, particles and Einstein !

Waves are something that have no mass and move at the maximum speed, mass m = 0. speed c = 1. So whats their momentum? p = m.v = 0? Right?

No. For pure waves; momentum does not come from mass. It comes only from motion.

(pure wave; they do not have mass)

For matter waves, on the other hand, momentum comes in two ways, mass as well as motion.

(impure, now they have mass)

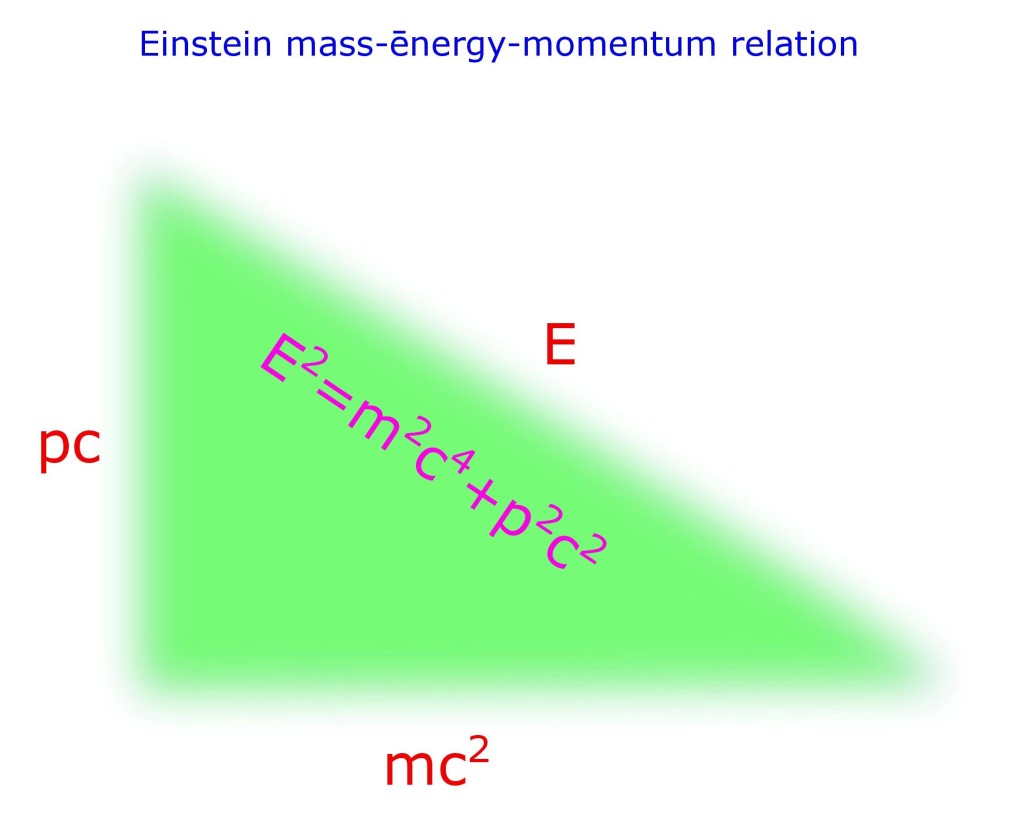
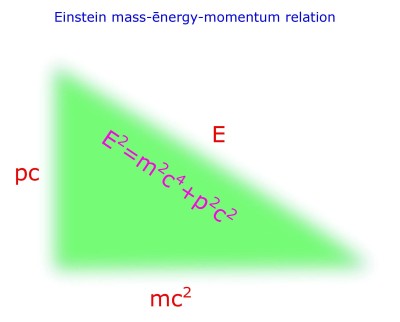
Albert Einstein recognized this fact and derived his relation;

This relation is called as Einstein’s relativistic equation, also Einstein’s mass-energy relation. But more appropriately  mass-energy-momentum relation.

Let us  consider E as the hypotenuse, p and m; as base or perpendicular as is your choice.

Then  is Pythagoras Theorem; when p is momentum and m is mass.

For pure waves such as photon … the quanta of light, m = 0.

Hence the Pythagorean Triangle is now one, where the mass side is arbitrary small. Thus E = p.

(A triangle with two sides because one side is as small as we wish)

This E = p relation is called as on-shell condition. A reason why nothing moves faster than waves. People have a habit of saying nothing is faster than light for this reason, as; light is also wave.

So in general, Energy is equivalent to mass (m) and momentum (p). And not just mass, as is popularly held.

What happens when you say; I divide Energy into two parts E1 and E2, such that E1 corresponds to m and E2 to p.

Then E = E1 = m comes only when there are particles that are not moving, so p = 0, note that this is never the case with what I called as waves or pure waves, such as photons. Photons will always have non zero p and zero m. As a consequence E1 = 0, E = E2 = p.

In the E = E1 = m case we say energy is equivalent to mass. Since, E = m, this is called as; Einstein’s mass-energy equivalence relation. Also written as E = m.c-square.

(Also E = p can be written as E = p.c)

People always say this and never care to mention in general; energy is equivalent to momentum and mass, that is energy comes from mass content as well as motion.

For pure waves, thus, energy is equivalent to momentum only. As we saw above E = p.

Thus m = 0 does not make momentum zero. Momentum equals to energy and comes from waves. Waves are constantly moving, at speed 1, that is; 3.00 x 10 ^ 8 m/s.

All particles, in the Universe, thus; lie in-between m = 0 and v = 1.

So photons are more wave like (in Q-Mechanics) because they have zero mass. But electrons which have a small mass are more particle like, than waves, even if both photons and electrons are supposed to be wave-particles in terms of Q-Mechanics.

That is why the more mass one has the more particle like one will behave, even though inherently one has wave properties as per Q Mechanics.

Although de–Broglie connects momentum to wavelength of particles, for pure waves such as photons or very small mass particles, the momentum coming from mass is very small or zero. So they show wave properties based on their energy = momentum, and not momentum coming from mass.

But for more and more massive particles the motion is at very low speed, compared to maximum 1 = 300,000 km/s, the momentum would be coming from mass.

A stone, say of mass 20 gm, thrown at 20 m/s, hardly shows any wave behavior. Its wave momentum is conspicuously lacking, due to heavy mass. But an electron, moving at 10% of speed of light has appreciable wave behavior because its mass is quite quite small and its closer to actual pure waves like photon. It has significant wave momentum even though momentum due to mass could be almost negligible.

That last remark is a bit tricky because one has to do actual calculation, but I am highlighting the idea, for the above discussion.