M Dash Foundation: C Cube Learning

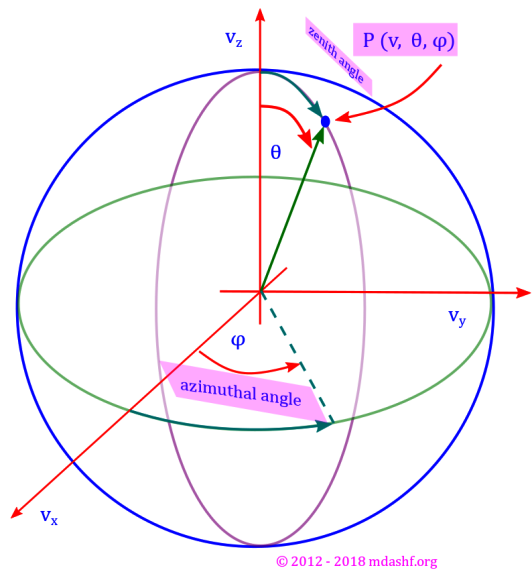
Tag: spherical polar coordinate

  • Laplace And Poisson Equation, Lecture 5, 6, 7 And 8.

    Laplace And Poisson Equation, Lecture 5, 6, 7 And 8.

    We will discuss 4 lecture hours of Laplace and Poisson Equation, their spherical coordinate forms and applications , boundary value problems in both spherical and Cartesian systems, there are 7 problems that are discussed in all details apart from required derivations.

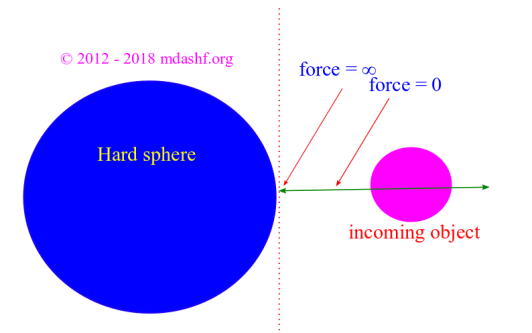
  • Maxwell Boltzmann distribution for a classical ideal gas

    Maxwell Boltzmann distribution for a classical ideal gas

    i. We assume a dilute gas which is enclosed by a thermally insulated container on all sides. Dilute gas in a thermally insulated container: Dilute means concentration of gas molecules is low. Insulated implies there is no reasonable flow of heat energy across the walls of the container. ii. Each molecule is assumed to be a…