Laplace And Poisson Equation, Lecture 5, 6, 7 And 8.

Lectures on Electricity and Magnetism — new series of lectures – EML – 5, 6, 7, 8.

All articles in this series will be found here. Click on link to left or search for menu “E AND M BASICS” on top.

Laplace And Poisson Equation; Boundary Value Problems, Applications And Solved Problems, Lecture 5, 6, 7, 8.

In our last lecture (EML-4) we discussed the conservative nature of the static electric field which also meant such fields are irrotational vector fields (that means their curl is zero). This led us to the formulation of electrostatic potential energy and electrostatic potential. Today we will see how this leads us further and lands us into the land of opportunities where we can solve, using the gained insights and relations a treasure trove of physical problems in electrostatics. We will study few examples of the usefulness of the knowledge we gained so far.

Recapitulation: In our first lecture in this series which can be found here; EML1, we laid a good foundation about the concepts of electric field, lines of force, flux and Gauss Law. In the second one (EML2) we discussed how to apply Gauss Law to find the electric field if cylindrical or planar symmetries are present in the problem, we solved the case of an infinitely long uniformly charged rod and an infinitely large non-conducting sheet of uniform charge. In the 3rd one (and EML3) we discussed how to do the same if spherical symmetry is present e.g. in the case of a spherical shell with uniform charge and a non-conducting spherical solid with uniform charge in its entire body.

+ click to see more about this article

This article belongs to a group of lectures I intend to prepare for their online dissemination — these were delivered in a physical format, beginning with hand written notes that were delivered in a classroom full of students. This series is on Electricity and Magnetism and bears the name sake Electricity and Magnetism Lectures and the number of the lecture will be appended to the end to reflect the same. eg the current lectures will be named EML – 5, 6, 7, 8 . A part of this lecture was delivered to honors students on 10th Feb 2017 and rest were taught later to different classes on 16 and 17th May 2019.

In the meanwhile if you can’t wait and you need some of these concepts at the earliest, here is a slide-share presentation I had made roughly 5 years ago that consists of “some of the things” an undergrad needs: Electricity and Magnetism slides. There are other slides on different topics at that account of mine on slideshare.net (such as; Introduction to Quantum Mechanics , and these are quite well received by the community for their usefulness).

Laplace And Poisson Equation

Integral Form Of Gauss Law

We saw in our previous lecture that electrostatic fields can be written as the (negative) gradients of scalar function Φ (called electrostatic potential): $\vec{E}=-\vec{\nabla} \Phi$ . We also saw in our first lecture (EML1) the integral form of the Gauss law: $\oint \vec{E}\cdot d\vec{S}=\Phi_E=\frac{Q_{encl}}{\epsilon_0}$ .

Gauss Divergence Theorem and Differential Form Of Gauss Law

We will now convert the integral form of Gauss law into its differential form, a veritably useful form at times, where the former won’t do. For this we need the Gauss divergence theorem (Gauss invented all his tools in-house didn’t he?). The Gauss divergence theorem relates the flux of a vector field through a closed surface to the divergence of the field in the volume bounded by the surface, mathematically: $\int_V (\vec{\nabla}\cdot \vec{E})dV=\oint_S \vec{E}\cdot d\vec{S}$ .

We realize that the total charge enclosed in the volume V is nothing but the volume integral of the volumetric charge density ρ, i.e. $Q_{encl}=\int_V \rho(\vec{r}) dV$ . This appears on right hand side of Gauss law (above), so we can equate the divergence theorem (for the electrostatic field) and the integral form of Gauss law and obtain: $\int_V (\vec{\nabla}\cdot \vec{E})dV=\frac{1}{\epsilon_0}\int_V \rho dV$ . This gives us the differential form of Gauss law: $\boxed{\vec{\nabla} \cdot \vec{E}=\frac{\rho}{\epsilon_0}}$ .

Poisson Equation

We saw that the consequence of having a conservative vector is that its also irrotational (i.e. its curl is zero), in-fact we mentioned that due to Helmholtz theorem these two facts are concurrent, i.e. one ensures the other. Thus our conservative electrostatic field leads to its curl being zero: $\vec{\nabla} \times \vec{E}=0$ . Using the fact that ( $\vec{E}=-\vec{\nabla} \Phi$ ) into differential form of Gauss law we get: $\boxed{{\nabla}^2 \Phi= - \frac{\rho}{\epsilon_0}}$ . Thus Gauss law took the form of this second order differential equation, and this very famous expression is known as Poisson Equation. ∇² is known as the Laplacian (or Laplacian operator).

Laplace Equation

If Φ is considered in a region, where there are no sources of electric charge, the charge density ρ is zero, in such regions. Then Poisson equation becomes the Laplace equation: $\boxed{{\nabla}^2 \Phi= 0}$ .

What happens to the curl equation: $\vec{\nabla} \times \vec{E}=0$ ? To inspect this we use the potential definition of the electrostatic field ( $\vec{E}=-\vec{\nabla} \Phi$ ) into the curl of the field and see that: $\vec{\nabla} \times \vec{E}=\vec{\nabla}\times (-\vec{\nabla} \Phi)$ . The right hand side of this expression is identically zero for all values of Φ as curl of a gradient is always zero.

This means the curl equation does not supply anything special or any additional information other than what we already have, viz, the Poisson equation. Why is this so? Because we used the curl equation to find the potential formulation of the electrostatic field so the gradient of that potential merely restates or confirms the curl equation. This is what Helmholtz theorem states, as we have discussed already.

Advantage of Poisson Equation

Poisson equation is a differential equation. It determines Φ which is a scalar field, so only one equation is sufficient. On the other hand E which is a vector field needs two equations, the divergence equation called Gauss law $\boxed{\vec{\nabla} \cdot \vec{E}=\frac{\rho}{\epsilon_0}}$ and the curl equation $\vec{\nabla} \times \vec{E}=0$ which makes the electrostatic field E a conservative field.

Solution to Poisson Equation

We can find solution to the Poisson equation if we know charge distribution ρ as a function of position. In general: $\boxed{\Phi(\vec{r})=\int d^3\vec{r}\,' k \frac{\rho(\vec{r}\,')}{|\vec{r}-\vec{r}\,'|}}$ . Since Laplace (charge free) equation is a second order differential equation, we need values of Φ and its first order derivative at some points to determine the solution. The values of Φ and its first order derivative as given values at some points are known as Boundary Value Conditions (BVC).

Laplace Equation in Spherical Polar Coordinates

Spherical Symmetry

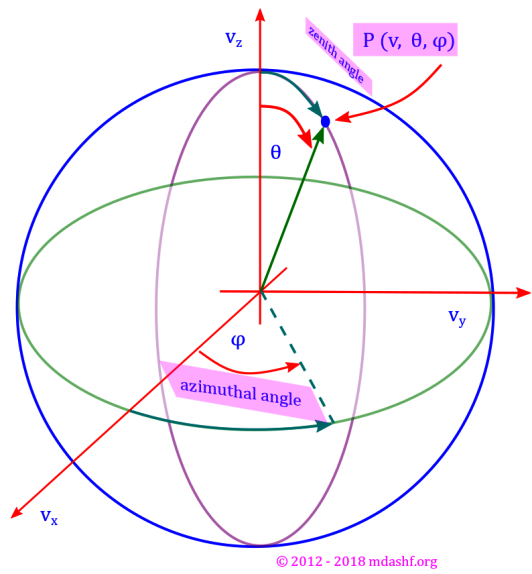
Any problem that involves a spherical symmetry (one where the results don’t change with change in angular direction but changes exclusively with radial distance) entails a spherical polar coordinate system for the easiest analysis. Hence we will cast the Laplace equation into its spherical polar form and suggest its general solutions in terms of Legendre polynomials, before solving some actual problems with spherical symmetry and more. The following diagram shows the spherical polar coordinate system, here v is a vector whose Cartesian values are v_x, v_y and v_z and its spherical polar components are v, θ and φ where v is the magnitude of v.

Spherical polar coordinates: azimuth angle ( φ ) zenith angle ( θ ) and vector magnitude variable (radial component, here r)

Laplace equation involves the Laplacian (∇²) and by employing the form of Laplacian in the spherical polar coordinates, we can write the following expression for the Laplace equation for the electrostatic potential Φ: $\boxed{\frac{1}{r^2}\frac{\partial}{\partial r}\bigg(r^2 \frac{\partial \Phi}{\partial r}\bigg) + \frac{1}{r^2 \sin \theta} \frac{\partial}{\partial \theta}\bigg(\sin \theta \frac{\partial \Phi}{\partial \theta}\bigg) +\frac{1}{r^2 \sin^2 \theta}\frac{\partial^2 \Phi}{\partial \phi^2} =0}$ .

Azimuthal Symmetry

If the problem has azimuthal symmetry i.e. potential Φ does not depend on azimuthal angle φ; Φ(r, θ , φ) = Φ(r, θ), then the spherical coordinate form of the Laplace equation reduces to one that involves differentiation wrt r and θ only and is given by: $\boxed{\frac{\partial}{\partial r}\bigg(r^2 \frac{\partial \Phi}{\partial r}\bigg) + \frac{1}{\sin \theta} \frac{\partial}{\partial \theta}\bigg(\sin \theta \frac{\partial \Phi}{\partial \theta}\bigg) =0}$ .

Variable Separable Method

This is amenable to the variable separable method of solving a differential equation. In fact r, θ , φ dependence is also amenable to the variable separable, but now we will deal with the simpler case of r, θ dependence only. We therefore assume a solution in the form of factorizable parts: Φ(r, θ) = R(r) Θ(θ). Following the basic rules of differentiation of a product of a function to a constant factor, we can write: $\frac{\partial \Phi}{\partial r}=\frac{\partial R(r)}{\partial r} \Theta (\theta)$ and $\frac{\partial \Phi}{\partial \theta}=R(r) \frac{\partial \Theta (\theta)}{\partial \theta}$ . We can substitute these into the reduced Laplace equation in the spherical system and divide by: Φ = RΘ.

We get: $\frac{1}{R}\frac{d}{dr}\big(r^2 \frac{dR}{dr}\big) + \frac{1}{\Theta \sin \theta} \frac{d}{d\theta}\big(\sin \theta \frac{d\Theta}{d\theta} \big)=0$ . We see that the first term here is solely a function of r and the second of θ. In order to split them into two separate differential equations where the functions (and derivatives) vary solely in one variable, we need to set each term to the same constant (with a minus sign to add to zero).

We have accordingly: radial part $\frac{1}{R}\frac{d}{dr}\big(r^2 \frac{dR}{dr}\big) =l(l+1)$ and zenith part $\frac{1}{\Theta \sin \theta} \frac{d}{d\theta}\big(\sin \theta \frac{d\Theta}{d\theta} \big)=-l(l+1)$ .

The radial equation is $\boxed{\frac{d}{dr}\big(r^2 \frac{dR}{dr}\big) =l(l+1)R}$ and it has a general solution given by: $\boxed{R(r)=A r^l + \frac{B}{r^{l+1}}}$ . Similarly the angular equation (azimuthal) is given by: $\boxed{\frac{d}{d\theta}\big(\sin \theta \frac{d\Theta}{d\theta} \big)=-l(l+1)\sin \theta \Theta }$ with Legendre Polynomials as solutions, stated as: $\boxed{\Theta(\theta)=P_l (\cos \theta)}$ .

Legendre Polynomial

The Legendre Polynomials P_l(x) are defined by the Rodrigue’s formula (with x = cos θ): $P_l(x)=\frac{1}{2^l l!}\big(\frac{d}{dx}\big)^l(x^2-1)^l$ . Few of them are stated here explicitly; $P_0(x)=1$ , $P_1(x)=x$ , $P_2(x)=\frac{3}{2}(x^2-1)$ , $P_3(x)=\frac{1}{2}(5x^3-3x)$ , $P_4(x)=\frac{1}{8}(35 x^4-30x^2+3)$ and $P_5(x)=\frac{1}{8}(63x^5-70 x^3-15x)$ .

P_l(x) is a lth order polynomial in x, it contains only even powers if l is even and only odd powers if l is odd. $P_l(x)=\frac{1}{2^l l!}$ is normalization constant so P_l(1)=1. There exists 2 solutions for each value of l, but the second solution blows up for θ = 0, π. hence it is discarded. So with azimuthal symmetry the electrostatic potential is given by: $\boxed{\Phi(r, \theta)= \sum_{l=0}^{\infty} \Big(B_l r^l + C_l r^{-l-1}\Big) P_l(\cos \theta)}$ .

Boundary Value Problem in Uniform Electric Field.

Now we are in a position to solve boundary value problems. We will illustrate the method in spherical system for the following three problems.

A Simple Spherical Symmetry Problem

Problem 1: For some spherically symmetric distribution of charge, the potential on the surface of a sphere of radius R is given to be V₀. Calculate the potential in the region r > R. Also calculate the potential in the region r < R, when no charges are present inside the sphere.

There is spherical symmetry in the problem so potential Φ must depend only on radial distance r and independent of the angular dimensions: θ and φ. As a result: $\Phi(\vec{r})=\Phi(r)$ . We can solve such problems easily in spherical polar coordinates. We saw above that the Laplace equation is given as the following in spherical polar coordinates: $\frac{1}{r^2}\frac{\partial}{\partial r}\Big(r^2 \frac{\partial \Phi}{\partial r}\Big) + \frac{1}{r^2 \sin \theta} \frac{\partial}{\partial \theta}\Big(\sin \theta \frac{\partial \Phi}{\partial \theta}\Big) +\frac{1}{r^2 \sin^2 \theta}\frac{\partial^2 \Phi}{\partial \phi^2}=0$ . 2nd and 3rd terms must vanish since potential Φ does not depend upon: θ and φ.

This leads to a simpler form for the Laplace equation: $\frac{d}{dr}\Big(r^2 \frac{d \Phi(r)}{dr}\Big)=0$ . Lets integrate this equation once: $r^2 \frac{d \Phi(r)}{dr}=A$ . Upon integrating the resulting expression: $\Phi(r)=-\frac{A}{r}+B$ . A and B are arbitrary constants to be determined from boundary value conditions.

Region I: (i.e. r ≥ R) No charges are present at ∞ so Φ(∞) = 0 ⇒ Φ(∞) = 0 = B. $\Phi(r)\big|_{r=R}=V_0$ ⇒ Φ(R) = V₀ = -A/R ⇒ A = -V₀R. So, $\Phi(r)\big|_{r\ge R}=\frac{V_0 R}{r}$ .

Region II: (i.e. r ≥ R) No charges are present in this region so ⇒ Φ(r) = -A’/r + B’. At r = 0, Φ has to be finite, this is possible if A’ = 0. ⇒ Φ(r) = B’. At r = R, Φ = V₀ ⇒ B’= V₀. So Φ(r) = V₀.

Dielectric Sphere In A Uniform Electric Field

Problem 2: A uniform electric field $\vec{E}=E\hat{z}$ exists in the z direction, throughout space, as shown in the figure. A sphere of dielectric constant ε and of radius R is introduced with its center at the origin. Calculate the electric field outside and inside of the sphere.

A sphere of dielectric constant ε and of radius R is introduced with its center at the origin into a uniform electric field that exists in the z direction, throughout space, as shown in the figure. We would like to determine the electric field everywhere using Laplace equation.

Azimuthal Symmetry

We have azimuthal symmetry due to the sphere and the electric field as the system has axial independence. If we rotate the sphere about z-axis (electric field is aligned along this axis) the result won’t change. That means changing the azimuthal coordinate φ from one value to another won’t change the result, so: Φ(r, θ , φ) = Φ(r, θ). We have seen this above and called this azimuthal symmetry. Hence we can use the results that we derived above.

Application of Solution to Laplace equation; Outside Sphere

For r > R i.e. outside region of the sphere there are no free charges, hence Laplace equation: ∇²Φ = 0 is satisfied. We have seen above that solution for Laplace equation with azimuthal symmetry is given by: $\Phi(r, \theta)=\sum_{l=0}^{\infty} \Big(B_l r^l + C_l r^{-l-1}\Big)P_l(\cos \theta)$ . The constants B_l and C_l are to be determined by imposing boundary conditions.

Boundary Conditions

BC 1: All induced charges are at finite values of r hence introduction of the dielectric sphere won’t change the existing uniform field $\vec{E}=E\hat{k}$ at far away distances. i.e. the original uniform along z-axis electric field retains its form at distances far away from the dielectric sphere. $\vec{E}= -\vec{\nabla} \Phi$ ⇒ $\Phi(r, \theta)= -Ez = -Er\cos \theta$ for r → ∞.

Lets apply this boundary condition to the general solution to Laplace equation. We get: B₁ r cos θ = -E r cos θ. We see that r^-l-1 = 0 if r → ∞ and l = 1 gives non-zero B_l, B_l = 0 if l ≠ 1 so B₁ = -E. Thus the solution looks like: $\boxed{\Phi(r, \theta)= -Er \cos \theta - \sum_{l=0}^{\infty} \Big(C_l r^{-l-1}\Big)P_l(\cos \theta)}$ .

Lets apply boundary conditions inside of the dielectric sphere (and on it), i.e. r ≤ R, there are no free charges, Laplace equation is satisfied, like before. But the solution to the Laplace equation now is given by a new set of constants B_l^‘ and C_l^‘. Solution for r < R; $\Phi(r, \theta)=\sum_{l=0}^{\infty} \Big({B_l}' r^l + {C_l}' r^{-l-1}\Big)P_l(\cos \theta)$ .

BC2: At origin (r = 0) the potential must be finite as there are no point charges there, this means C_l^‘ for all l must be set to zero.

BC3: The potential must be continuous across r = R, i.e. across the surface of the spherical dielectric material, due to absence of free charges. So the solution for r > R that we obtained and the one we obtained above for r ≤ R must be set equal.

$\boxed{\Phi(r, \theta)= -ER \cos \theta - \sum_{l=0}^{\infty} \Big(C_l R^{-l-1}\Big)P_l(\cos \theta)=\sum_{l=0}^{\infty} \Big({B_l}' Rr^l \Big)P_l(\cos \theta)}$ .

BC4: We know the boundary conditions to be imposed on fields when they pass through material media, and we have discussed this here. We will use that result by remembering that normal vector component of the vector D is continuous across boundary r = R as there are no free charges at that interface. i.e. $\boxed{\vec{D}=\epsilon \vec{E}=-\epsilon \vec{\nabla}\Phi}$ is continuous at r = R so $\frac{\partial \Phi}{\partial r}\big|_{outside} =K\frac{\partial \Phi}{\partial r}\big|_{inside}$ where K = ε is the relative permittivity or dielectric constant. So we have: $\boxed{-E \cos \theta - \sum_{l=0}^{\infty} C_l(-l-1) R^{-l-2}P_l(\cos \theta)=K\sum_{l=0}^{\infty} l{B_l}' R^{l-1}P_l(\cos \theta)}$ .

Orthogonality Properties of Legendre Polynomials: The Legendre Polynomials satisfy the following orthogonality and normality properties: $\boxed{\int_{-1}^{1} P_l(\cos \theta)P_m(\cos \theta)d(\cos\theta)=\frac{2}{2l+1}\delta_{lm}}$ . We multiply the two equations we got from boundary conditions (BC3 and BC4) by P_m(cos θ) and integrate over cos θ from -1 to +1. We obtain: $\int_{-1}^{1} ER\cos\theta P_m(\cos \theta)d(\cos\theta)-C_mR^{-m-1}\Big(\frac{2}{2m+1}\Big)=\frac{2}{2m+1}B_m'R^m \,\,\,eq^n-1$ and $\int_{-1}^{1} E\cos \theta P_m(\cos \theta)d(\cos\theta)-C_mR^{-m-2}(-m-1)\Big(\frac{2}{2m+1}\Big)=K\frac{2}{2m+1}mB_m'R^{m-1} \,\,\, eq^n-2$ . With P₁(cos θ) = cos θ, $\int_{-1}^{1} \cos\theta P_m(\cos \theta) d(\cos\theta) =\int_{-1}^{1}P_1(\cos \theta)P_m(\cos \theta)d(\cos\theta) =\frac{2}{3} \delta_{m1}$ .

Now we multiply eqⁿ-1 by (-m-1) and eqⁿ-2 by R and subtract, to get; $-\frac{2}{3}(-m-2)ER\delta_{m1}=\frac{2}{2m+1}R^mB_m'(-m-1-Km)$ . So we obtain: $\boxed{B_1'=-\frac{3E}{2+K},\,\,\, B_m'=0,\,\,\, m\ne1}$ . We substitute this into the condition obtained in BC3. $-\frac{2}{3}ER\delta_{m1}-C_m R^{-m-1}\Big(\frac{2}{2m+1}\Big) = -\Big(\frac{2}{2m+1}\Big)\frac{3E}{2+K}R\delta_{m1}$ which gives us: $\boxed{C_m=0,\,\,\, m\ne1,\,\,\, C_1=-ER^3\Big(\frac{K-1}{K+2}\Big) }$ .

We now have all the required constants and so the solutions for the electrostatic potential for the given problem, both inside and outside the dielectric sphere.

$\boxed{\Phi(r, \theta)=-Er\cos \theta + ER^3\Big(\frac{K-1}{K+2}\Big)r^{-2} \cos \theta,\,\,\,r>R}$ and $\boxed{\Phi(r, \theta)=-\Big(\frac{3E}{2+K}\Big)r \cos \theta,\,\,\,r<R}$ . We represent the situation with two diagrams.

A uniform electric field along the z-axis

When a dielectric sphere is placed in an otherwise uniform electric field, the filed lines are modified near the sphere due to induced charges on the sphere, but straighten out to their original form far away from the sphere,

Uncharged Metal Sphere In A Uniform Electric Field

Problem 3: An uncharged metal sphere of radius R is placed in an otherwise uniform electric field $\vec{E}=E_0\hat{k}$ as shown in the figure. Find the potential in the region outside the sphere.

The field will push positive charge to the upper i.e. northern surface of the sphere and negative charges will be pushed to the lower or southern surface. The surface of the sphere is an equipotential surface (as metals are conductors). We can choose this equipotential value to be zero.

The potential Φ does not go to zero for large values of z. Far from the sphere, field is $E_0 \hat{k}$ hence potential is: Φ = -E₀z + C. Φ must be zero in the equatorial plane (xy plane, z = 0 i.e.), due to symmetry (equal charges on either side). This means C = 0.

The boundary conditions are

i. Φ = 0 when r = R.
ii. Φ→ -E₀r cos θ, for r >> R

Solution: We have seen that our general solution has the form: $\Phi(r, \theta)= \sum_{l=0}^{\infty} \Big(A_l r^l + B_l r^{-l-1}\Big)P_l(\cos \theta)$ . From Boundary Condition i (BC-i) $A_l R^l + B_l R^{-l-1}=0$ or $B_l = -A_l R^{2l+1}$ , so: $\Phi(r, \theta)= \sum_{l=0}^{\infty} A_l \Big( r^l - \frac{R^{2l+1}}{R^{l+1}}\Big) P_l(\cos \theta)$ . For r >> R, 2nd term → 0. Also from BC-ii $A_l r^l P_l(\cos \theta)=-E_0 r \cos \theta$ . Thus only l = 1 term must be present. As P_l(cos θ) = cos θ, A₁ = -E₀ and A_l = 0 if l ≠ 1. Conclusion: $\boxed{\Phi(r, \theta)= -E_0\Big(r - \frac{R^3}{r^2}\Big)\cos \theta}$ . 1st term represents the external field. 2nd term is due to induced charge contribution.

Induced Charge Density: Now we can give a word about the induced charge density: $\boxed{\sigma(\theta)= -\epsilon_0\frac{\partial \Phi}{\partial r}\Big|_{r=R}= \epsilon_0 E_0\Big(1+2\frac{R^3}{r^3}\Big)\cos \theta\Big|_{r=R} =3\epsilon_0 E_0\cos \theta}$ . The induced charge density is +ve in northern hemisphere (0 ≤ θ ≤ π/2) and -ve in southern hemisphere (π/2 ≤ θ ≤ π).

Now we will turn our gaze into a problem with a different symmetry than spherical or azimuthal symmetry. Sometimes we need to employ both Laplace and Poisson equation in a given problem. The following is an example.

Infinite Planar Symmetry

Problem 4: Let A, B, C and D be infinite planar surfaces. A and D are at zero potential. Region between B and C has charges with a constant charge density ρ. The separation between A and B, between B and C and between C and D are d, 2t and d respectively. Calculate the electrostatic potential between A and B, between B and C and between C and D.

We begin with the following simple diagram that represents the situation.

The diagram shows 4 infinite parallel planar surfaces with their boundary value conditions specified. We would like to determine the electrostatic potential between each pair of planes, using the Laplace equation in rectangular Cartesian coordinate system.

The normal to the surfaces is along z-axis, mid point between B and C is at z = 0. The potential depends only upon z (due to planar symmetry it does not depend upon x and y). Let V₁, V₂ and V₃ be the potential between A & B (region 1), between B & C (region 2) and between C & D (region 3) respectively. Lets use the Cartesian coordinate system, where Laplacian has the following form: $\nabla^2 = \frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}+\frac{\partial ^2}{\partial z^2}$ .

The potential equations are either Laplace equation or Poisson equation: $\frac{d^2 V_1}{dz^2}=0$ in region 1, is Laplace Equation, $\frac{d^2 V_2}{dz^2}=-4\pi k \rho$ in region 2, is Poisson Equation and $\frac{d^2 V_3}{dz^2}=0$ in region 3, is Laplace Equation.

To find their solutions we integrate each equation, and obtain: V₁ = C₁z + C₂, V₂ = C₃z + C₄ – 4πkρz²/2 and V₃ = C₅z + C₆. According to the boundary value conditions at z = d + t and z = -d – t the potential is zero at these surfaces. This gives C₂ + C₁(d + t) and C₆ + C₅(-d – t). Thus V₁ = C₁(-z -d -t) and V₃ = C₅(z + d + t).

Another boundary value condition is at z = t the potentials are continuous so V₁ = V₂ and $\frac{dV_1}{dz}=\frac{dV_2}{dz}$ . This gives -C₁ d = C₃t + C₄ – 4πkρt²/2 and C₁ = C₃ – 4πkρt. Similarly at z = -t the potentials are continuous so V₂ = V₃ and $\frac{dV_2}{dz}=\frac{dV_3}{dz}$ . This gives C₅d = -C₃t + C₄ – 4πkρt²/2 and C₅ = C₃ + 4πkρt.

Solutions For The 3 Potentials: Now we can solve for the constants C₁, C₃, C₄ and C₅ by elimination. We eliminate C₁ from first two equations, and C₅ from last two equations. We obtain: C₃(t + d) + C₄ = 4πkρ(t²/2 + td) and C₃(t + d) – C₄ = -4πkρ(t²/2 + td). This gives us C₃ = 0, C₄ = 4πkρ(t²/2 + td), C₁ = -4πkρt and C₅ = 4πkρt. Thus we have the 3 solutions given by: V₁ = -4πkρt(z – d – t), V₂ = 4πkρt(t/2 + d) – 4πkρz²/2, V₃ = 4πkρt(z + d + t).

Solved Problems on Boundary Value Conditions and Laplace/Poisson Equation.

Now we will solve a few boundary value problems on the Laplace and Poisson equation before wrapping up this longish lecture. Aptly 4 lecture hours has been devoted to this article, but it helps to put certain things together.

Problem 5: In a one dimensional device the charge density is given by, ρ_v = ρ₀x/a. If E = 0 at x = 0 and V = 0 at x = a, find V and E using Poisson Equation of electrostatics.

In 1 dimension the Poisson’s equation takes the form: $\nabla^2 \Phi = \frac{\partial^2 \Phi}{\partial x^2}=-\frac{\rho_v}{\epsilon_0}=-\frac{\rho_0}{\epsilon_0} \frac{x}{a}$ . We integrate this once and obtain: $-\frac{\partial \Phi}{\partial x}=\frac{\rho_0 x^2}{2a\epsilon_0}+C f(y,\,z)$ . according to the given boundary value condition: $|\vec{E}|=-\frac{\partial \Phi}{\partial x}=0 \,\,\,@x=0$ ⇒ $0 = 0+ C f(y,\,z)$ . This is true if: C = 0. So we find the expression for Electrostatic field i.e. electric field: $\boxed{ E= |\vec{E}| = \frac{\rho_0 x^2}{2a\epsilon_0}}$ .

We integrate the above solution for electric field once again to get the electrostatic potential: $\Phi=-\int\frac{\rho_0 x^2}{2a\epsilon_0}dx + D f(y,z)$ to obtain: $\Phi=-\frac{\rho_0 x^3}{6a\epsilon_0} + D f(y,z)$ . The other boundary value condition that is given states that: Φ = 0 @ x = a ⇒ $0 =-\frac{\rho_0 a^2}{6\epsilon_0}+D f(y,\,z)$ ⇒ $Df(y,\,z) = \frac{\rho_0 a^2}{6\epsilon_0}$ . This gives us the expression for the electrostatic or electric potential as well: $\boxed{\Phi=\frac{\rho_0}{6\epsilon_0}(a^3-x^3)}$ .

Problem 6: What is the volume density of charge in a region of space where electrostatic potential is given by V = a – b(x² + y²) – c log (x² + y²), where a, b, c are constants?

The Poisson equations reads as: $\nabla^2 V = -\frac{\rho}{\epsilon_0}$ . In Cartesian coordinates this takes the form (as we saw above in Problem 4): $\nabla^2 V= \frac{\partial ^2 V}{\partial x^2}+\frac{\partial ^2 V}{\partial y^2}+\frac{\partial ^2 V}{\partial z^2}=-\frac{\rho}{\epsilon_0}$ . The potential V is given as: V = a – b(x² + y²) – c log (x² + y²) ⇒ $\frac{\partial V}{\partial x}=-2bx- \frac{2cx}{x^2+y^2}$ . Now the second order partial derivative is obtained from the first order. $\frac{\partial^2 V}{\partial x^2}=-2b- 2c\frac{y^2 - x^2}{(x^2+y^2)^2}$ . Similarly we obtain: $\frac{\partial V}{\partial y}=-2by- \frac{2cy}{x^2+y^2}$ and $\frac{\partial^2 V}{\partial y^2}=-2b- 2c\frac{x^2 - y^2}{(x^2+y^2)^2}$ . Also first and second order partial derivatives of potential V wrt z are simply zero (there is no z dependence). Using all these into the Poisson equation gives us the volume charge density: ρ = 4ε₀b.

Problem 7: Verify whether the electric potential V = 15x²yz – 5y³z, satisfies Laplace equation or not?

Laplace equation in Cartesian coordinate system reads as: $\frac{\partial ^2 V}{\partial x^2}+\frac{\partial ^2 V}{\partial y^2}+\frac{\partial ^2 V}{\partial z^2}=0$ . For the given potential V = 15x²yz – 5y³z, $\frac{\partial V}{\partial x}=30xyz$ , $\frac{\partial^2 V}{\partial x^2}=30yz$ . Similarly we obtain: $\frac{\partial V}{\partial y}=15x^2z-15y^2z$ and $\frac{\partial^2 V}{\partial y^2}=-30 yz$ and $\frac{\partial V}{\partial z}=15x^2y-5y^3$ and $\frac{\partial^2 V}{\partial z^2}=0$ . All teh 3 second order partial derivatives add up to zero, hence the given potential satisfies Laplace equation.

Rate this:

Comments

One response to “Laplace And Poisson Equation, Lecture 5, 6, 7 And 8.”

Uniqueness Theorem in Electrostatics – M Dash Foundation: C Cube Learning

July 16, 2020

[…] and Poisson equations are discussed in much detail (with derivation, applications and problems) here in EML-5, 6, 7 and […]

LikeLike

Laplace And Poisson Equation, Lecture 5, 6, 7 And 8.

Laplace And Poisson Equation; Boundary Value Problems, Applications And Solved Problems, Lecture 5, 6, 7, 8.

Laplace And Poisson Equation

Integral Form Of Gauss Law

Gauss Divergence Theorem and Differential Form Of Gauss Law

Poisson Equation

Laplace Equation

Advantage of Poisson Equation

Solution to Poisson Equation

Laplace Equation in Spherical Polar Coordinates

Spherical Symmetry

Azimuthal Symmetry

Variable Separable Method

Legendre Polynomial

Boundary Value Problem in Uniform Electric Field.

A Simple Spherical Symmetry Problem

Dielectric Sphere In A Uniform Electric Field

Azimuthal Symmetry

Application of Solution to Laplace equation; Outside Sphere

Boundary Conditions

Uncharged Metal Sphere In A Uniform Electric Field

Infinite Planar Symmetry

Solved Problems on Boundary Value Conditions and Laplace/Poisson Equation.

Rate this:

Share this:

Comments

One response to “Laplace And Poisson Equation, Lecture 5, 6, 7 And 8.”

Leave a comment Cancel reply