Why is Energy Conserved? — originally created, July 01, 2012.
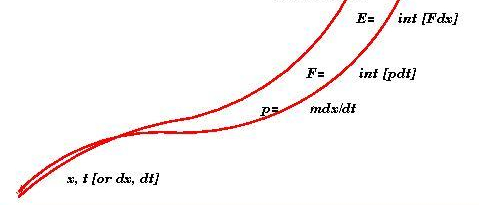
Action in Physics defined as . Note that we have used E to mean a specially defined form of energy. The usual definition is in terms of L which stands for Lagrangian.
We can also use the definition of the Hamiltonian form for energy, H. The difference between these two formulations is given by: E = T – U — for Lagrangian and E = T + U — for the Hamiltonian fashionistas.
The T and U stands for the kinetic energy and potential energy respectively for any kinematic system.
The above diagram then makes an attempt to envisage how any differential of energy would permeate to a system, given we know or can set a differential equation of motion by defining basic parameters of a kinematic (mechanical) system.
One can see that any loss or gain in Energy or Lagrangian etc is permeated in steps through lower order integrals or differentials, these are marked on the diagram. We surmise that all these information are inbuilt in the equation of motion which is derivable from the Principle of least or stationary action.
In-fact this visualization can very well represent the case for time dilation or contraction as a conceptual consequence.
We can say Energy or more fundamentally action distributes itself through the equation of motion, which as we know is a differential equation obtained by application of principle of stationary action through the method of calculus of variation to the Hamiltonian action integral.
Let us now return to the far simpler proposition of law of conservation of energy with a prospect of this formalism of Physics in mind.
Why is energy conserved? Is there something called principle of attraction?
Why is energy conserved?
Well, everything is conserved. Are you not?
Are you nuts?
No I am not.
What are you not, conserved or nuts.
I don’t know, you con-fusing me.
You called me a con.
You confused me and called me a nuts.
I didn’t confuse you. It was the conversation.
Well, why did you ask two questions; when one hasn’t been answered yet.
Well, I didn’t ask two. You asked one of them.
Which one?
I don’t remember. Lets go back.
I don’t wanna.
If you don’t wanna, I don’t wanna.
And, this is where the band starts its music.
Is there something called Principle of Attraction? Lets review, what we mean. I never heard that attraction factor, in, physics. Nobody said it to me. So, I would bet; it does not exist.
And, I would call you a lunatic, for imagining diamonds in air, 笑, and proposing the world to harness it. Are you looking for funds, for it? Well, you know, if we can find the diamonds, then guess what, we will pay back the funds, and we will still have enough to cruise around the world.
Well here is what it is.
The Physics. The Physics inc. The Physics inc. defines its ways. But, unlike Mississippi girl; it changes its ways. Physics inc changes its ways, but nobody gets it.
Here is the way; that hasn’t been changed in a long time. We, start with a simple object, and we note that, such an object is defined for its motion by whats called, its location in space = x, or, the increments in its location, which is called, an infinitesimal distance = dx, the instantaneous time at which its motion is referred, t, or, the increments in its time, called dt.
Thats it. And, we would like to know; all that the object does in terms of x, t.
I would not like it, if my dear people sit in a car, and it vanished into thin air and never came back. I would like to keep track of it, the car, because I know my people would still be in it. I would like to, keep track of satellites, and, missiles and airplanes, I would like to know, whats happening around me, and why its happening.
It all started, with the quest, to solve for the trajectory, and then, became more complicated, as the complexity of these objects or systems grew. Collectively, they satisfy greatly, the quest we had set on, since the millennium and more, to understand, whats all, that goes on, in our universe, in our close vicinity, and in situations far off from us, as far as the extraneous bounds of the galaxy, in which we live, and more and more and more and deeper and deeper.
Then, x, t are not sufficient, to describe such situations. But, since its all systematic, we know all that has been defined, its not a party or Ramstein Music Band, where you forgot what happened yesterday. Its Hello Physics Inc. Pay Attention.
Now, as we defined dx and dt, we also note that, their ratio, or as-is-called, rate of x wrt t, called speed = v, is often formally written, as, x with a dot on it, . Its the first order time derivative of x =
. Then comes its derivative
= acceleration.
We also form, two quantities;
1. from v we form m.v = p = momenta, by multiplying the mass m into the velocity or speed v.
2. from a, we form in the same way, F = m.a = force.
But, force is also defined to be the time-rate of change of momentum p, or in other words, the ratio of the increments dp and dt, .
This latter is called Newton’s 2nd law; .
Its called a law, but strictly speaking, its a mathematical law so far, and not one which describes, universe’s phenomena so it cannot be called, a physical law or principle as of yet.
This point was originally raised by Feynman; as far as I know.
will be a physical law, when, force is well defined — eg in terms of its dependence on space and time and their higher increments, and the differential equation as obtained from
leads to a viable solution and explains some observed characteristics.
Since, , we also note that
and, somewhere here impulse gets defined, perhaps impulse is the integrand F.dt. I recall I was in high-school when I first learned this, 20 years ago and refreshing this is hard job.
Impulse tells us, a rapidness of a force as the time could be defined to be very short it can be used to compare rapidness of different forces. A bomb will shatter you, and obviously the gross impulse is 1000s of time more than, a knock by your friend. Hence, so much caution, for bombs. And, terrorists for this reason alone, can be called impulsive.
Now that we have force F, and its a time-rate of change-of-momentum p — also , time derivatives are denoted by dots, we also have, a quantity whose derivative is force F.
But, this time its a derivative w.r.t. space or location x. So, force is called a space-gradient, as its a space-derivative of a quantity, called energy. So, energy — for comparison,
, or we can differentiate, and have
.
Note that E can come, in various forms, from its special form called kinetic energy T — or K.E. or K, or its general form called potential energy called U — sometimes also, V or P.E. Which is exactly why we can also say, theory of relativity is categorized as special and general theory of relativity.
Special theory pertains to speed v only, hence, and, general theory pertains to potential energy of all sorts, not just gravity, gravity is a special case of general theory, interestingly enough, described in an article written by me yesterday; What is Theory of Relativity.
When I said E can come in various form, I meant it can come as work, internal energy, heat, radiation and so on. Work is defined as .
Also, its very interesting, you will note in the above, if you are attentive, that, and
evidently means; E and p are equivalents in theory of relativity as x and t are.
This means (x, t) and (p, E) are 4-vectors in theory of relativity, this also means, this integration itself transforms as a 4-vector equation, under Lorentz transformation. Recognize this, from any text book, and let me know. I haven’t ever studied many advanced text of Physics.
So, some hints of relativity, are already there, in old classical mechanics although, we might not have noticed, if Einstein didn’t work everything out. — In addition you may want to read the couple of articles, recently written by me, that tells why much of relativistic ideas were present in old classical mechanics, and this is nothing new to relativity of Einstein, although their exact forms changed, in whats now called, Einstein’s Relativity Theory or loosely Relativity Theory.
So to write a summary of these definitions:
space and time points, and their differentials; x, t, dx, dt, ,
differentials of speed, acceleration; ,
momentum — from “lower” speed and “higher” force; ,
force — from “lower” acceleration and “higher” energy-work; ,
energy-work — from “lower” force; ,
energy — in two useful forms; L = T – U, H = T + U
Action — gets defined from “lower” energy; in two forms, as an integral.
Thats the end of physics formalism.
By lower we mean differential and by higher we mean integral.
where U = U (x, t, v, a), an explicit function of the variables in parenthesis and each quantity, can depend on the other, through relations or laws that are valid in nature. Its just in this statement one can recognize, there is some concepts of relativity theory or as I expounded in the previously linked article “What is Theory of Relativity”, equivalence theory; U = potential energy is equivalent to energy, coming from x, t, v and a.
In-fact potential energy comes from our location or configuration, as functions of time, hence x, t and it depends on the speed of our frame-of-reference v, or in other words, one needs to account for kinetic energy, from the total energy H, and get U, or one can also have; an equivalent form of energy, coming from acceleration.
If a system is accelerated, there is some unaccounted energy, compared to the situation when the a = 0 ≡ uniform velocity, which is how, everything has been formulated, so unaccounted changes were accommodated by defining and, we truncate this change, by saying there is no
.
What if or, a = constant. Why are forces always constant or are they?
We have been solving Newton’s equation of motion — and not Newton’s law: F = m.a, thanks Feynman, explained above, by; assuming forces that are not changing in time.
If they are changing, such changes are already included, by integrating w.r.t. time, and, if its changing over space, we are integrating over space — as per the concept of force-field,
.
In other words, we have defined a quantity called energy, such that, its sitting at the top of everything so far, on the top of: x, t, v, p, a, F. Any change will be accommodated into energy.
What about a change in speed v affecting E? What about a change in acceleration ‘a’ affecting E? That is — 1st derivative and 2nd derivative of space, wrt time, not completely accounting for the energy.
Then; energy would not be conserved.
The answer perhaps lies in two “facts”.
Reason one.
We solve each equation of motion in a particular system, know as many forces as we know, and define in terms of the above, kinematic and dynamical quantities, and see if everything is fine. If not, may be we are missing a force, or not taking effects into account. If we can solve, based on this formalism, we have almost always gotten our best answers, although there may be a few anomalies, loopholes or unsolved problems.
Summary of what I said: before giving you the 2nd reason.
Let me give you a few more quantities; that are used when solving physical problems. Since U is a function of x, t, v, a etc and U is equivalent to energy, which strictly depends on the noninertialness, rotation or pseudo forces etc and T is a very special form of energy and also used to specify the frame of reference, with the caution, that, in relativity theory mass is no more a constant and the recognition that the other variables described here, may also be functions of such: x, t, v, a etc we have a formalism in place.
— Einstein just didn’t like leaving any variable to be assumed as constant — such as mass, and pulled out of equations, but started differentiating them and applied a few of his insights and grossly enough, changed the course of Physics.
So instead of assuming that mass is a constant, as has been assumed for centuries preceding him, he considered it as a variable and differentiated it, using a product rule of differentiation and showed that, with his insights such as speed-of-light is a constant in wave theory of light, mass must depend on speed of objects.
This is also a cursor to , as, given a speed we have an energy. Basically he segregated the equivalent relations by being careful enough.
Add to that, the following idea, first. Like, we defined energy as a total force, we can define action as a total energy, but this time, integrated w.r.t. time. Energy is a total force in space and action is a total energy in time.
In other words sometimes we integrate w.r.t. space and sometimes we integrate w.r.t. time. So we have action is total force in space and time.
In the formalism of physics, action is the prime-most variable. If we solve a differential equation, by using Newton’s law scheme, which is a specialized system-specific approach, we get solutions to the differential equation — called as an “equation of motion”, but the more powerful method would be, the principle of action, because it does not leave quantities unattended. Action is then like Einstein.
Reason two.
Whats then the 2nd reason for why energy would not be conserved? Perhaps the above, that some quantities, may not only be left unattended by applying heuristic methods such as that of Newton’s 2nd law, but also by allowing the possibility that this action principle itself, may also be leaving variables unattended. Who knows?
Here are the rest of the quantities, that will perhaps make the formalism a little more comprehensive. There are fields, defined from the forces, by dividing the charges or masses — electric field E is electric force F per charge q and — potential V is potential energy U per mass m. Gravity is just a special example of a potential energy and we have gravitational force, gravitational potential, gravitational potential energy and so on.
Some more quantities are thusly E, B, Φ and A. Actually B is a field like E field — or its corresponding force, potential or potential energy etc can also be invoked, Φ and A come as an alternative formulation of E and B, these are called scalar and vector potential respectively.
So these — Φ and A, are potentials, which are either scalar or vector quantities and by treating them as potentials we can, from our ensuing formalism, get the E and B fields. Potential is energy by charge or mass and then needs to be differentiated to get force and divided again by charge or mass to get the fields B, E.
But the advantage is what is called Gauge formalism symmetry. In this way a variety of Φ and A will produce the same E and B. But since changing Φ and A did not change E and B but made the purported solutions much easier to deal with, this is called a gauge symmetry. In this technique the physics remains unchanged but the mathematics one has to deal with is considerably simplified.
Symmetry refers to the situation when an underlying quality or quantity remain the same, even when we submit them to some kind of transformations or change. In this case, Φ and A changed, underlying quantity E and B did not, so Gauge transformation refers to the change in Φ and A and Gauge symmetry refers to the invariance of E and B. Gauge is the name of a lady in the cyber world and physics has got nothing to do with it.
But note that Φ and A still conform to our hello physics inc. formalism. They are potentials. Also they satisfy whats called a wave equation. From the concepts of a wave one can define wavelength: λ, wave number: k, frequency: ν or f and time period T.
One can have a phase, an amplitude which is the maximum difference of the wave disturbance from its mean vantage of disturbance. Probably we do not have any more quantities in the formalism. Well probability, but that comes when we allow the wave to be a complex number function.
So by applying least variations on action S one gets a bunch of differential equations — for various systems and solves them. These equations are called equations of motion. If they are defined for an object with localized attributes its called simply as an equation of motion.
If the object or system is not localized but have extended attributes then the differential equation is called wave equation of motion, but still it comes from action principle.
If the object has a dual-attribute it is both localized and extended, obviously not necessarily both at the exact same instant of time, this latter fact being known as the complementarity principle of quantum mechanics*, then the action principle gives us whats called a wave-particle equation of motion, Schrodinger’s equation or wave equation of motion in quantum mechanics.
*Obviously as a name sake because wave compliments a particle and vice versa but they do not replace each other or appear at the same time because that will make them the same object, either localized or extended ones and one would lose the dual-attribute.
Interestingly enough as I had noted recently — and dwelled upon it for sometime, I had asked such a question several years ago: why the Schrodinger’s equation of motion is a 1st order time derivative but a 2nd order derivative in space? where as the wave equation of motion of classical mechanics is a 2nd order time and 2nd order space differential equation?
Thats because the particle equation of motion or simply the equation of motion in classical mechanics is a 1st order time derivative — along with 2nd orders as well of time, equation. So a wave-particle equation has to be 1st order time derivative: at-least that is a good hint.
Here are their forms:
Particle: — 1st order differentials in time; .
Wave: — only 2nd order in space and time; .
Wave-particle: — again 1st order in time, oops … there must be a particle here, 2nd order in space? OK there is a wave here too; , where
.
OK the list of quantities is not yet finished. We are gonna have angular momentum and this is listed into two types: spin and orbital. And energy, angular momentum, linear momentum p etc are sometimes called as constants of motion.
In some motions p is conserved, in some J = L + S is conserved. Note that L is not the Lagrangian — = T – U, and S is not action, both as defined earlier in this article, but L is orbital angular momentum, S is spin angular momentum and J is total angular momentum.
It is said that energy E is always conserved, which is what this article wanted to explore.
I am thinking any more quantity?
OK perhaps not.
The quantities that are conserved are connected to Noether’s theorem: for every symmetry transformation there is a corresponding quantity that is conserved and for every quantity thats conserved, there is a symmetry that corresponds to this or in other words: symmetry transformations and conservation are necessary and sufficient towards each other.
So p, J and E etc are associated with corresponding transformations.
eg p is conserved if space-translation symmetry is satisfied which means , or p = constant. Whats the big deal, nothing, its just a simpler form that we always studied.
Similarly J = constant if total external torque, is zero or there is rotational symmetry.
A space flipping is called a parity transformation which is associated with a parity symmetry — via Noether’s theorem, mentioned above. A space translation that leads to constant p is
, and a space rotation is
leading to constant J.
Energy is conserved if there is time-translation symmetry. A time translation, leads to energy conservation or constant energy.
But one shall recall that where E appears as total energy in two different forms, H or L. — Absence of T or U would make it a special case, E = T = kinetic energy say.
Since S is submitted to least variation under which it must remain “minimum and constant over various paths”any difference of time must not change E. So “energy conservation” is embedded into the “principle of action” or the latter would not be valid. They are perhaps necessary and sufficient for a good formalism to work.
But this is good enough to see why time translation is inherently connected to energy conservation. I have actually used least action principle to derive equivalence principle of Einstein — perhaps in a round about way which led to a simple insight that given to the constant of integration, T and U must be equivalents or in other words there is no difference in their nature, hence equivalence of T and U and hence equivalence of say inertial-mass and gravitational-mass.
As I have noted here and elsewhere the gravity is just a special case of potential energy U and it derives from acceleration = a in many forms, such as rotation or pseudo forces and there is nothing in action principle that suggests they must be different. That is acceleration being a form of energy and pseudo-acceleration being another they serve just like gravity.
There is nothing Einsteinian about gravity or equivalence principle — and even time dilation itself. Its energy that warps space, time, speed, acceleration etc and warping means not having a flattened appearance or attribute or quantity, this is the basis of ordinary motion. Just from this one can build theory of relativity in alternative ways.
In-fact I have obtained time dilation from a simple gravity force, without using Einstein’s relativistic concepts, I will post the calculations soon, but the ideas are described in article: Time dilation: energy slows down clocks … Newtonian time dilation.
Now that we see that energy conservation is evidently — manifestly, accommodated by the principle of stationary action we ask why energy is the highest level of a physical quantity that must be conserved. eg why not we stopped at p or J or even v.
Because we say these change when there are higher order changes present in the system or unaccounted. So we went on integrating to find the higher order variable and currently we have energy. But to note we integrated wrt either x or t, in steps. Hence so to say, Action is the total force — over all space and all time.
We never integrated wrt say v or a.
What if this way we account only for the action S thats fitting into our scheme. Perhaps nature has more and thats why our formalism are not the most consistent.
Lets define traction. Traction we integrate wrt v so
being a velocity derivative we called it traction.
Then we can define attraction this accommodates the changing accelerations and
. Attraction is the total force if you consider x, t, v and a not just x,t.
Then one can apply least attraction. A least attraction is what we are seeking in nature. We want to take that path for which attraction is the least and stationary over all available paths.
This formalism was neither thought nor explored ever. Perhaps this will lead to more physics insights, unless a mathematician proves us wrong by saying why according to mathematical concepts of now, we do not need so many variables.
Perhaps we need these variables and mathematics and with it some physics will be changed.
Thats all I wanted to say this after-noon about conservation of energy.
Leave a comment