The CSIR NET 2018 held on December 16: Indian Assistant Professor and PhD scholarship exam solution, prepared by me. The answers and detailed explanations are available for 18 out of 25 questions of Part-B. The detailed explanations and answers to Part-A is also available, see link below. Please point out any inadvertent errors. (this is entirely free stuff: help spread the word)

( CSIR NET 2018 December: Part A ) See the detailed explanations and solutions to part A

The article aims to make the best attempt at finding the answers for the recently concluded 2018 CSIR NET. Detailed explanatory answers for physical sciences section ( part-B ) is available ( for 18 out of 25 questions at the moment ). Also full explanation based solutions to part-A is available, check link above.

CSIR NET 2018 December physical sciences

Part B

Q - 21. Consider the decay A → B + C of a relativistic 
spin 1/2 particle A. Which of the following statements 
is true in the rest frame of the particle A?

1. The spin of both B and C may be 1/2.
2. The sum of the masses of B and C is greater than 
the mass of A.
3. The energy of B is uniquely determined by the 
masses of the particles. 
4. The spin of both B and C may be integral.
click to see or hide answer to Q – 21

— the answer is: option 3.

Explanation: obviously the second option is incorrect as it violates conservation of energy in relativistic kinematics, rest-masses of the product particles can not be more than that of the parent particle. Option 3 is explained with a diagram. The value of the energy of one of the daughter particle ( B ) is determined uniquely as evinced by the given formula for the same.

In a two body relativistic decay in the parent rest frame: EB = ( MA2 – MC2 + MB2 ) / 2 MA

Also the other options talk about the spin of the particles but we need not bother since option 3 is the correct option.

CSIR NET 2018 December Physical Sciences: answer to question 21, the two body decay. The energy and momenta of the daughter particles are uniquely determined in parent rest frame. Photo Credit: mdashf.org
CSIR NET 2018 December Physical Sciences: answer to question 21, the two body decay. The energy and momenta of the daughter particles are uniquely determined in parent rest frame. Photo Credit: mdashf.org

Hence the correct answer is option 3.

Q - 22. Two current-carrying circular loops, each 
of radius R, are placed perpendicular to each other, 
as shown in the figure below. the loop in the 
xy-plane carries a current I0 while that in the 
xz-plane carries a current 2I0. The resulting magnetic 
field \vec{B} at the origin is
CSIR NET 2018 December Physical Sciences: question 22. Photo Credit: mdashf.org
CSIR NET 2018 December Physical Sciences: question 22. Photo Credit: mdashf.org
1. \frac{\mu_0 I_0}{2R}[2\hat{j}+\hat{k}]\, 2. \frac{\mu_0 I_0}{2R}[2\hat{j}-\hat{k}]\,
3. \frac{\mu_0 I_0}{2R}[-2\hat{j}+\hat{k}]\, 4. \frac{\mu_0 I_0}{2R}[-2\hat{j}-\hat{k}]\,
click to see or hide answer to Q – 22

— the answer is: option 3.

We only need to find the direction of the net magnetic field of the two circular loops to be able to select the correct answer. Thats because all the options have the same common magnitude of the field: ( μ0 I0 ) / 2 R. For the vertical loop with current 2I0 if we curl our palm along the shown direction for current our thumb points in the – y axis. Thus we should have a vector:  -2\hat{j}. Similarly for the horizontal loop if we curl our palm along the shown direction for the current our thumb points in the +ve z axis and we must have a vector: \hat{k}. As a result the total field created by the two loops of currents is: \frac{\mu_0 I_0}{2R}[-2\hat{j}+\hat{k}]\,.

Hence the correct answer is option 3.

Q - 23. An electric dipole of dipole moment \vec{P}=qb\,\hat{i} 
is placed at the origin in the vicinity of 
two charges +q and -q at (L, b) and (L, -b)
respectively, as shown in the figure below. 
The electrostatic potential at the point 
(L/2, 0) is
CSIR NET 2018 December Physical Sciences: question 23. Photo Credit: mdashf.org
CSIR NET 2018 December Physical Sciences: question 23. Photo Credit: mdashf.org
1. \frac{qb}{\pi \epsilon_0}\big(\frac{1}{L^2}+\frac{2}{L^2+4b^2}\big) 2. \frac{4qbL}{\pi\epsilon_0[L^2+4b^2]^{\frac{3}{2}}}
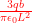
3. \frac{qb}{\pi \epsilon_0 L^2} 4. \frac{3qb}{\pi \epsilon_0 L^2}
click to see or hide answer to Q – 23

— the answer is: option .

Explanation:

Hence the correct answer is option .

Q - 24. A monochromatic and linearly polarised 
light is used in a Young's double slit 
experiment. A linear polarizer, whose pass axis 
is at an angle 450 to the polarisation of the 
incident wave, is placed in front of one of the 
slits. If Imax and Imin, respectively denote, 
the maximum and minimum intensities of the 
interference pattern on the screen, the visibility, 
defined as the ratio (Imax - Imin)/(Imax + Imin), is

1. √2/3                   2. 2/3  
3. 2√2/3                  4. √2/√3
click to see or hide answer to Q – 24

— the answer is: option 3.

Explanation: (updated 10:45 pm, 14-12-2019) For the time being I am uploading a scanned solution sheet. I will update this later. To understand the expressions you need to go through the linked lecture: ( lecture VII ) read about interference of light waves and remember how intensity is dropped by a square of cosine of angle between source polarization and polarizer pass axis. Remember that both intensity (slit 1 and slit 2) are same to begin with (I_zero). Then one of the intensity (either slit) is changed due to polarization through the polarizer. interference and YDSE

Hence the correct answer is option 3.

Q - 25. An electromagnetic wave propagates in 
a non-magnetic medium with relative permittivity 
ε = 4. The magnetic field for this wave is 
\vec{H}(x,y)= \hat{k}H_0 \cos(\omega t-\alpha x - \alpha \sqrt{3}y) where H0 is a constant. 
The corresponding electric field \vec{E}(x,y) is

1. \frac{1}{4}\mu_0 H_0 c(-\sqrt{3}\hat{i}+\hat{j})\cos(\omega t-\alpha x - \alpha \sqrt{3}y)
2. \frac{1}{4}\mu_0 H_0 c(\sqrt{3}\hat{i}+\hat{j})\cos(\omega t-\alpha x - \alpha \sqrt{3}y)
3. \frac{1}{4}\mu_0 H_0 c(-\sqrt{3}\hat{i}-\hat{j})\cos(\omega t-\alpha x - \alpha \sqrt{3}y)
4. \frac{1}{4}\mu_0 H_0 c(-\sqrt{3}\hat{i}-\hat{j})\cos(\omega t-\alpha x - \alpha \sqrt{3}y)
click to see or hide answer to Q – 25

— the answer is: option 1.

Explanation: the idea is to determine the direction of the \vec{E} field as the magnitude is same in all 4 given options. The first thing to calculate is the direction of the em wave. The direction of the em wave ( same as wave propagation vector and the direction of Poynting vector \vec{S} ) in a cos ( kx – ωt ) = cos ( ωt – kx ) variation is in the + x direction. This means our given wave travels in the direction of the vector (\sqrt{3}\hat{j}+\hat{i}). But we know that \vec{S}=\vec{E}\times \vec{H}. The option 1 gives us: (-\sqrt{3}\hat{i}+\hat{j}) \times \hat{k}=\sqrt{3}\hat{j}+\hat{i}. We used the fact that: direction of the magnetic field vector H/B is \hat{k}.

Hence the correct answer is option 1.

Q - 26. The ground state energy of an anisotropic 
harmonic oscillator described by the potential: 
V(x,y,z) = (1/2) mω2x2 + 2mω2y2 + 8mω2z2 
(in units of \hbar\omega )

1. 5/2               2. 7/2 
3. 3/2               4. 1/2
click to see or hide answer to Q – 26

— the answer is: option .

Explanation:

Hence the correct answer is option .

Q - 27. The product ΔxΔp of uncertainties in the 
position and momentum of a simple harmonic oscillator 
of mass m and angular frequency ω in the ground 
state |0\rangle , is \frac{\hbar}{2}. The value of the product ΔxΔp in the 
state e^{-i\hat{p}l/\hbar}|0\rangle  
( where l is a constant and \hat{p} is the momentum 
operator ) is

1. \frac{\hbar}{2}\sqrt{\frac{m\omega l^2}{\hbar}} 2. \hbar 
3. \frac{\hbar}{2} 4. \frac{\hbar ^2}{m\omega l^2}
click to see or hide answer to Q – 27

— the answer is: option .

Explanation:

Hence the correct answer is option .

Q - 28. Let the wavefunction of the electron in 
a hydrogen atom be \psi(\vec{r}) = \frac{1}{\sqrt{6}}\phi_{200}(\vec{r})+\sqrt{\frac{2}{3}}\phi_{21-1}(\vec{r})-\frac{1}{\sqrt{6}}\phi_{100}(\vec{r}), 
where \phi_{nlm}(\vec{r}) are the eigenstates of the 
Hamiltonian in the standard notation. The 
expectation value of the energy in this state is

1. -10.8 eV           2. -6.2 eV 
3. -9.5 eV            4. -5.1 eV
click to see or hide answer to Q – 28

— the answer is: option 4.

Explanation: the given state is already normalized ( amplitude squares add up to 1 ). All we need to do is compute ( amplitude ) 2 / n2 and multiply to -13.6 eV. The ( amplitude ) 2 and corresponding n2  are given as: ( 1/6, 4 ), ( 2/3, 4 ), ( 1/6, 1). This gives -5.1 eV, answer that is given in option 4.

Hence the correct answer is option 4.

Q - 29. Three identical spin 1/2 particles of mass m 
are confined to a one-dimensional box of length L, but 
are otherwise free. Assuming that they are 
non-interacting, the energy of the lowest two energy 
eigenstates, in units of \frac{\pi^2\hbar^2}{2mL^2}, are

1. 3 and 6                     2. 6 and 9
3. 6 and 11                    4. 3 and 9
click to see or hide answer to Q – 29

— the answer is: option 1.

Explanation: the energy eigenstates of the 1 dimensional box are given as: \psi = \sqrt{\frac{2}{L}}\sin \frac{n\pi}{L}x and the eigenvalues are given as n^2 \times \big(\frac{\pi^2\hbar^2}{2mL^2}\big). Accordingly the lowest two energy eigenstates correspond to the quantum numbers ( 1, 1, 1 ) where all the 3 particles are in the ground state and ( 2, 1, 1 ) where at-most 1 particle is in the first excited state and the other two in the ground state. Accordingly the lowest two energy states correspond to 12+12+12 = 3 and 22+12+12 = 6 in units of \frac{\pi^2\hbar^2}{2mL^2}.

Hence the correct answer is option 1.

Q - 30. The heat capacity CV at constant volume of 
a metal, as a function of temperature, is αT+βT3, 
where α and β are constants. The temperature 
dependence of the entropy at constant volume is  

1. αT+(1/3)βT3             2. αT+βT3 
3. (1/2)αT+(1/3)βT3        4. (1/2)αT+(1/4)βT3
click to see or hide answer to Q – 30

— the answer is: option 1.

Explanation: The specific heat at constant volume is given by the expression: C_V = T\big(\frac{\partial S}{\partial T}\big)_{N,\,V}. An integration of the same yields the temperature dependence of the entropy: S = [∫ (CV/T ) dT ]N, V = ∫α dT + ∫βT2 dT = αT + (1/3)βT3.

Hence the correct answer is option 1.

Q - 31. The rotational energy levels of a molecule
are E_l = \frac{\hbar^2}{2I_0}l(l+1) where l = 0, 1, 2, ... and I0 is its 
moment of inertia. The contribution of the rotational 
motion to the Helmholtz free energy per molecule, at 
low temperatures in a dilute gas of these molecules, 
is approximately 

1. -k_B T\big(1+\frac{\hbar^2}{I_0 k_B T}\big)             
2. -k_B T e^{-\frac{\hbar^2}{I_0 k_B T}}
3. -kBT        
4. -3k_B T e^{-\frac{\hbar^2}{I_0 k_B T}}
click to see or hide answer to Q – 31

— the answer is: option .

Explanation:

Hence the correct answer is option .

Q - 32. The vibrational motions of a diatomic 
molecule may be considered to be that of a 
simple harmonic oscillator with angular 
frequency ω. If a gas of these molecules is 
at a temperature T, what is the probability 
that a randomly picked molecule will be found 
in its lowest vibrational state? 

1. 1-e^{-\frac{\hbar \omega}{k_B T}}             
2. e^{-\frac{\hbar \omega}{2k_B T}}
3. \tanh\big(\frac{\hbar \omega}{k_B T}\big)
4. \frac{1}{2}cosech\,\big(\frac{\hbar \omega}{2k_B T}\big)
click to see or hide answer to Q – 32

— the answer is: option 2.

Explanation: when a system is in thermal equilibrium with a heat reservoir at temperature T, the probability Pr that the system be found in a state ( with index r ) with energy Er is given by this temperature T and energy of the state Er in the following manner ( its called canonical distribution ) : Pr = C e-βEr. Here β = (kBT)-1 and C is the constant which is the inverse of Z the sum of states or partition function ( C = Z-1 ) given by: Z = ∑r e-βEr. We can take C to be 1. What remains is the probability or the Boltzmann factor: e-βEr. So the probability of finding the randomly picked molecule in an energy state Er is e-(1/(kBT))Er. But energy of the diatomic molecules is given by: \big(n+\frac{1}{2}\big)\hbar \omega. In the ground state ( n = 0 ) the energy is: \big(\frac{1}{2}\big)\hbar \omega. Thus the probability of finding a randomly picked molecule in its lowest vibrational state is: e^{-\frac{\hbar \omega}{2k_B T}}.

Hence the correct answer is option 2.

Q - 33. Consider an ideal Fermi gas in a grand 
canonical ensemble at a constant chemical 
potential. The variance of the occupation number 
of the single particle energy level with mean 
occupation number \bar{n} is

1. \bar{n}(1-\bar{n})             
2. \sqrt{\bar{n}}
3. \bar{n}
4. \frac{1}{\sqrt{\bar{n}}}
click to see or hide answer to Q – 33

— the answer is: option 1.

Explanation: For a general statistical variable x the variance ( Δ which is the square of the standard deviation σ ) is given by: \Delta =Npq where p gives the probability of occurrence and q=(1-p) the probability of non-occurrence. Since we have a single particle we can safely take N = 1. This gives us the correct option when we realize that the probability of occurrence p is the same as the mean of the occupation number \bar{n}. Since grand canonical ensemble of a single fermion system is only a subsystem of the general statistical system this result follows. Other options can’t follow from this general formula. ( I have checked the answer to be correct, although there is a rigorous proof, but I am unable to plough further at the moment. )

Hence the correct answer is option 1.

Q - 34. Consider the following circuit, consisting of 
an RS flip-flop and two AND gates.
CSIR NET 2018 December Physical Sciences: question 34. Photo Credit: mdashf.org
CSIR NET 2018 December Physical Sciences: question 34. Photo Credit: mdashf.org
Which of the following connections will allow the 
entire circuit to act as a JK flip-flop?

1. Connect Q to pin 1 and \bar{Q} to pin 2          
2. Connect Q to pin 2 and \bar{Q} to pin 1
3. Connect Q to K input and \bar{Q} to J input
4. Connect Q to J input and \bar{Q} to K input
click to see or hide answer to Q – 34

— the answer is: option 2.

Explanation: let’s follow the figure. Also I have given the truth table for a JK flip-flop, for the enthused. ( One can verify the flip flop works correctly with the truth table. )

CSIR NET 2018 December Physical Sciences: converting a RS flip-flop into a JK flip-flop. Photo Credit: mdashf.org
CSIR NET 2018 December Physical Sciences: converting a RS flip-flop into a JK flip-flop. Photo Credit: mdashf.org
C ( clk )JKQn+1Action
↑00Qn (last)No change
↑010RESET
↑101SET
↑11\bar{Q}_n (toggle)Toggle

Hence the correct answer is option 2.

Q - 35. The truth table below gives the value Y(A,B,C) 
where A, B and C are binary variables.
ABCY
0001
0010
0100
0111
0001
0010
0100
0111
Truth table: gives the value Y(A,B,C) where A, B and C are binary variables. 
The output Y can be represented by

1. \bar{A}\bar{B}C+\bar{A}B\bar{C}+A\bar{B}C+AB\bar{C}
2. \bar{A}\bar{B}\bar{C}+\bar{A}BC+A\bar{B}\bar{C}+ABC
3. \bar{A}\bar{B}C+\bar{A}BC+A\bar{B}C+ABC
4. \bar{A}\bar{B}\bar{C}+\bar{A}B\bar{C}+A\bar{B}\bar{C}+AB\bar{C}
click to see or hide answer to Q – 35

— the answer is: option 2.

Explanation: Only option 2 satisfies all rows of the table. eg if we take row 1: A = 0, B = 0, C = 0. Their inversions are respectively 1, 1, 1 and we get Y = 1+ 0+0+0=1 which is also shown in the table. Let’s take the first row of table and apply on option 1. We see Y = 0. But table says 1. Hence option 1 can’t be correct. Similarly easily it can be checked that option 3 and 4 are incorrect.

Hence the correct answer is option 2.

Q - 36. A sinusoidal signal is an input to the 
following circuit.
CSIR NET 2018 December Physical Sciences: Question 36 Photo Credit: mdashf.org
CSIR NET 2018 December Physical Sciences: Question 36 Photo Credit: mdashf.org
Which of the following graphs best describes the 
output waveform?
CSIR NET 2018 December Physical Sciences: Question 36 options Photo Credit: mdashf.org
CSIR NET 2018 December Physical Sciences: Question 36 options Photo Credit: mdashf.org
click to see or hide answer to Q – 36

— the answer is: option .

Explanation:

Hence the correct answer is option .

Q - 37. A sinusoidal voltage having a peak value of Vp 
is an input to the following circuit, in which the DC 
voltage is Vb.
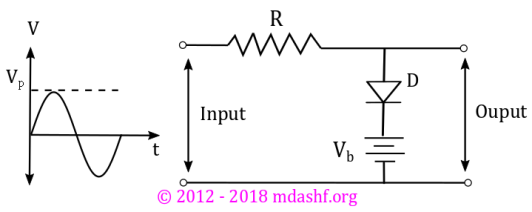
CSIR NET 2018 December Physical Sciences: Question 37 Photo Credit: mdashf.org
CSIR NET 2018 December Physical Sciences: Question 37 Photo Credit: mdashf.org
assuming an ideal diode, which of the following best 
describes the output waveform?
CSIR NET 2018 December Physical Sciences: Question 36 options Photo Credit: mdashf.org
CSIR NET 2018 December Physical Sciences: Question 37 options Photo Credit: mdashf.org
click to see or hide answer to Q – 37

— the answer is: option .

Explanation:

Hence the correct answer is option .

Q - 38. One of the eigenvalues of the matrix eA is ea, 
where A = \begin{pmatrix}a & 0 & 0 \\ 0 & 0 & a \\ 0 & a & 0 \end{pmatrix}. The product of the other two 
eigenvalues of eA is 

1. e2a              2. e-a
3. e-2a             4. 1
click to see or hide answer to Q – 38

— the answer is: option 4.

Explanation: To solve this we need to know 2 identities of the elegant matrix method. one: det (eA) = eTr (A) two: the product of eigenvalues of eA = det (eA). Since Tr (A) = a therefore we see that the product of eigenvalues of eA = ea. Thus the product of the other two eigenvalues is just 1.

Hence the correct answer is option 4.

Q - 39. The polynomial f(x) = 1 + 5x + 3x2 is written 
as a linear combination of the Legendre polynomials
(P0(x) = 1, P1(x) = x, P2(x) = (1/2)(3x2 - 1))
as f(x) = Σn cnPn(x). The value of c0 is

1. 1/4            2. 1/2
3. 2              4. 0
click to see or hide answer to Q – 39

— the answer is: option 3.

Explanation: Let’s write f(x) = c0P0(x) + c1P1(x)  + c2P2(x) = 1 + 5x + 3x2. This means c0+c1x+c2(3x2–1)/2 = 1 + 5x + 3x2 and c0-(c2/2)=1, c1=5, (c2)×(3/2) =3.  Solving for c2 this gives: c2 = 2. Solving for c0 gives c0 = 2.

Hence the correct answer is option 3.

Q - 40. The value of the integral \oint_C \frac{dz}{z}\frac{\tanh 2z}{\sin \pi z}  where C is 
a circle of radius π/2, traversed counter-clockwise, 
with centre at z = 0, is 

1. 4               2. 4i
3. 2i              4. 0
click to see or hide answer to Q – 40

— the answer is: option 4.

Explanation: According to the residue theorem: \oint_C f(z)\,dz=2\pi i \times \sum (residues\,of\,f(z)\,inside\,C). Here: f(z)=g(z)/zh(z) where g(z) = tanh z and h(z) = sin πz. We see that f(z) has a simple pole at z = 0, h(0) = 0 and g(z) is analytic. So residue is given as: R(0) = lim z→0 [zf(z)]= lim z→0 [zg(z)/(zh(z))]. Then by L’Hospital’s rule: R(0) = g(0) lim z→0 [1/h(z)] = g(0) lim z→0 [1/h'(z)]=g(0)/h'(0) = 0/1=0. So the integral is zero.

Hence the correct answer is option 4.

Q - 41. A particle of mass m, moving along the 
x-direction, experiences a damping force -γv2, 
where γ is a constant and v is its instantaneous 
speed. If the speed at t = 0 is v0, the speed 
at time t is  

1. v0e-(γv0t)/m                 2. v0/{1+ln[1+(γv0t)/m]}
3. mv0/(m+γv0t)               4. 2v0/[1+ e(γv0t)/m]
click to see or hide answer to Q – 41

— the answer is: option 3.

Explanation: from the given information we can write: m(d2x/dt2) = -γv2 so m(dv/dt) = -γv2 and (mdv)/v2=-γdt. Integrating and using given initial conditions ( v = v0 at t = 0 ) we get option 3: v = mv0/(m+γv0t).

Hence the correct answer is option 3.

Q - 42. The integral I = ∫c ezdz is evaluated 
from the point (-1,0) to (1,0) along the 
contour C, which is an arc of the parabola
 y = x2 - 1, as shown in the figure.
quest42
CSIR NET 2018 December Physical Sciences: question 42. Photo Credit: mdashf.org
The value of I is 

1. 0                  2. 2 sinh 1
3. e2i sinh 1         4. e + e-1
click to see or hide answer to Q – 42

— the answer is: option .

Explanation:

Hence the correct answer is option .

Q - 43. In terms of arbitrary constants A and B, 
the general solution to the differential equation 
 x2(d2y/dx2) + 5x(dy/dx) + 3y = 0 is 

1. y = A/x + Bx3      2. y = Ax + B/x3 
3. y = Ax + Bx3      4. y = A/x + B/x3
click to see or hide answer to Q – 43

— the answer is: option 4.

Explanation: it can be easily checked that 1/x and 1/x3 satisfy the given differential equation hence a linear combination of them viz. y = A/x + B/x3 also satisfies the differential equation.

Hence the correct answer is option 4.

Q - 44. In the attractive Kepler problem described
by the central potential V(r) = -k/r ( where k is a 
positive constant ), a particle of mass m with a 
non-zero angular momentum can never reach the center 
due to the centrifugal barrier. If we modify the
potential to V(r) = -k/r - β/r3 one finds that there
is a critical value of the angular momentum lc 
below which there is no centrifugal barrier. This 
value of lc is 

1. [12km2β]1/2            2. [12km2β]-1/2
3. [12km2β]1/4            4. [12km2β]-1/4
click to see or hide answer to Q – 44

— the answer is tentative: option 1.

Explanation: k has units of ( energy × distance ) / mass and β has units of  ( energy × volume ) / mass. So [12km2β]1/2 has units of energy × area. Angular momentum has units of energy × time. So option 1 seems to be close to the correct answer ( I am guessing: other options have energy units in the square root or inverse ). Or something is missing.

Hence the correct answer seems to be option 1.

Q - 45. The time period of a particle of mass m, 
undergoing small oscillations around x = 0, in the 
potential V = V0 cosh (x/L), is 

1. \pi \sqrt{\frac{mL^2}{V_0}}    2. 2\pi \sqrt{\frac{mL^2}{2V_0}}
3. 2\pi \sqrt{\frac{mL^2}{V_0}}   4. 2\pi \sqrt{\frac{2mL^2}{V_0}}
click to see or hide answer to Q – 45

— the answer is tentative: option 3.

Explanation: F = -dV/dx = -V0/L sinh (x/L). For small oscillations sinh (x/L) ~ x/L. So, F  = -(V0x/L2) = -kx. So, k = V0/L2. So time period is given as: 2\pi \sqrt{m/k}=2\pi \sqrt{\frac{mL^2}{V_0}}.

Hence the correct answer is option 3.

One thought

  1. Pingback: The CSIR NET 2018 December solutions – M Dash Foundation

Leave a Reply

Please log in using one of these methods to post your comment:

Gravatar
WordPress.com Logo

You are commenting using your WordPress.com account. ( Log Out /  Change )

Facebook photo

You are commenting using your Facebook account. ( Log Out /  Change )

Cancel

Connecting to %s