Category: interference
-
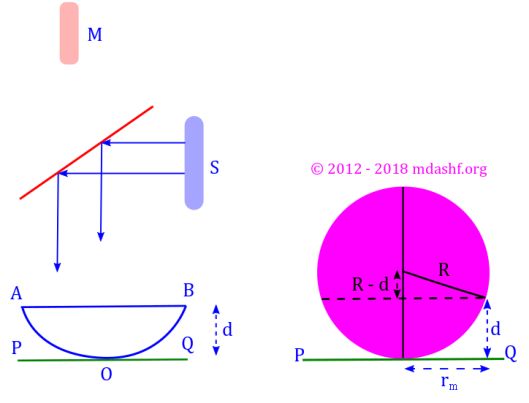
Interference of two types
Interference by wave-front and amplitude splitting. Optics Series Lecture, Lecture – XIV, XV, XVI. Topics covered in this lecture A. Color of thin films B. Newton’s rings C. Lloyd’s mirror and D. Phase changes during reflection We have previously discussed what is interference and what are wave-front splitting and amplitude splitting interference. We have also discussed…
-
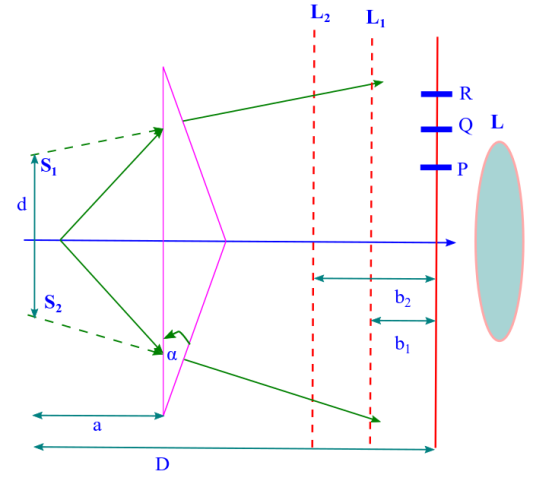
Fresnel’s Bi-prism; measurement of wavelength of light
Optics Series Lecture, Lecture – XI “Fresnel’s Bi-prism: measurement of wavelength of light by it.” Today we will discuss another interesting interference set-up, now that we have discussed the Young’s double slit experiment, in lecture – IX. A few words about the general mechanism behind interference. There are two kinds of interference basically that we…
-
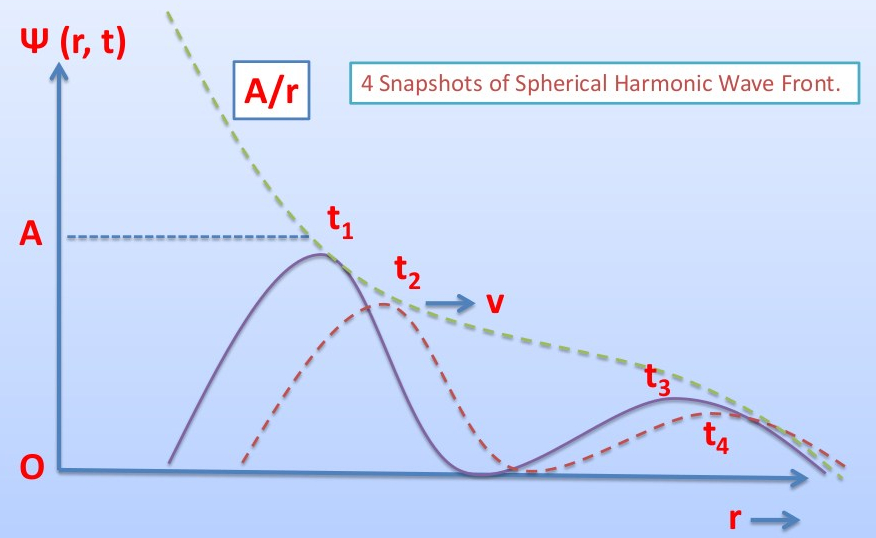
Spherical harmonic waves
In our lecture — VIII, we worked out the form of plane harmonic traveling waves. Note that soon we will have to a. address the concept of wave profile and b. how to convert a wave profile into its corresponding time-dependent or traveling form. But before we do that here is yet another general form of…
-
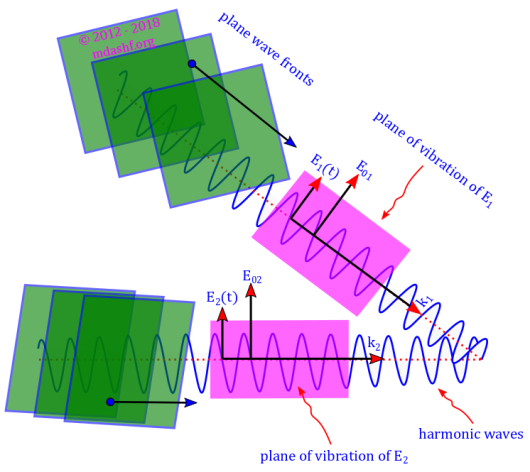
Interference of two plane harmonic waves
Optics Series Lecture, Lecture – VII. “Conditions of interference, Interference of two plane harmonic waves.” This lecture was delivered on 7th February in a lecture session of 1 and 1/2 hours. This lecture was delivered to Physics elective students but intended as a lecture towards Honors students at a later date. Electromagnetic Waves. Light is…
M Dash Foundation: C Cube Learning 