Category: Invariance @MDashF
-
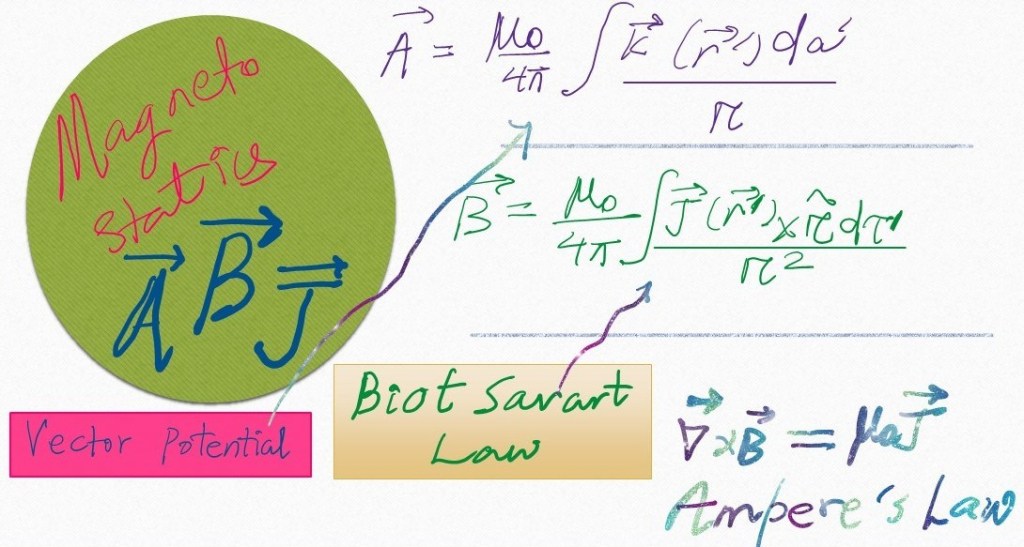
Magnetic vector potential of a rotating uniformly charged shell.
Today we will solve the problem of finding magnetic vector potential of a rotating, uniformly charged spherical shell. We won’t discuss the general idea behind the vector potential (how it follows from Helmholtz theorem, and gauge freedom etc) and how its defined. That will be part of a conceptual lecture and will be available when…
-
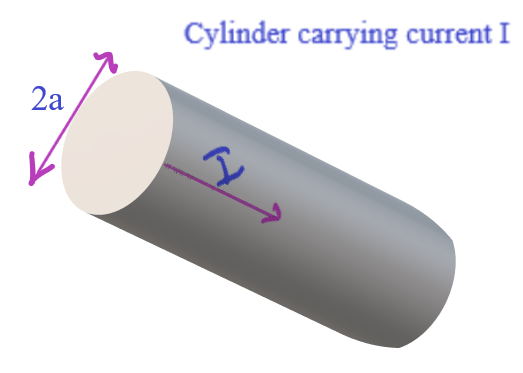
Problem 5.13 Application of Ampere’s Law.
Yesterday we saw an interesting application of the Ampere’s Law (– in magnetostatics and sometimes called Ampere’s circuital law also) for the infinite uniform surface current. Today we will see yet another display of the elegance and efficacy of this law in the following problem. This problem is inherited from Griffith’s text on Electrodynamics (3rd…
-
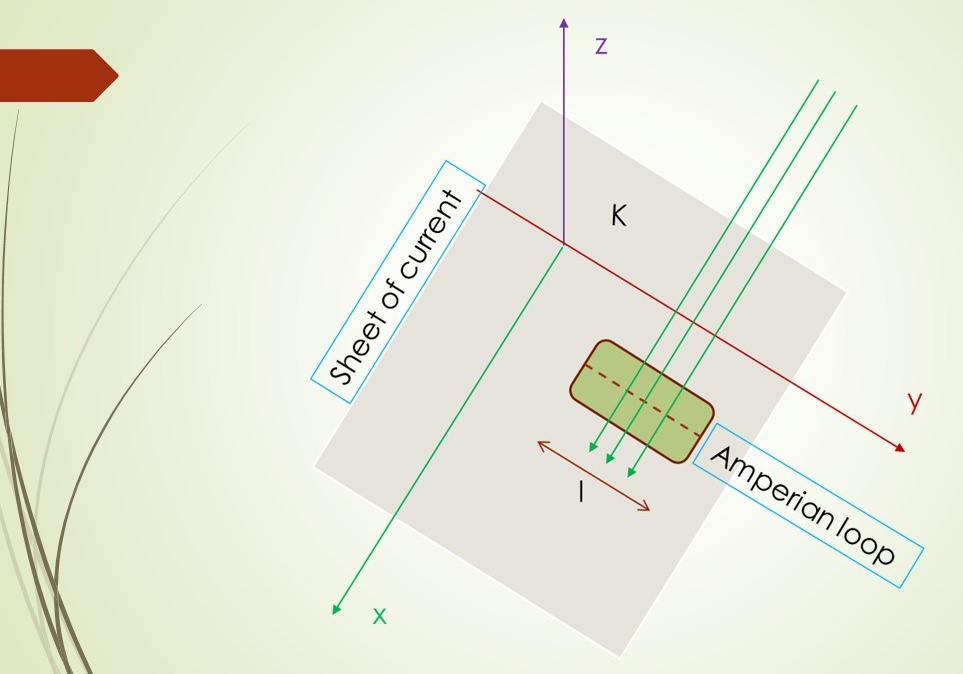
Example 5.7; Application of Ampere’s law.
The following problem is an interesting application of Ampere’s law apart from usual applications found in honors syllabus (eg infinite straight conductor, Solenoid and Torroid). This is to be found the excellent book by Griffith on Electrodynamics. Find the magnetic field of an infinite uniform surface current K (vect) = K i-cap, flowing over the…
-
Why light would curve under gravity?
Everyone was thinking in terms of physics (i.e. force). Einstein knew one part of that is maths, pure maths. Force is physics because of mass. But acceleration is geometry, its the shape of your trajectory and its maths. Imagine a pipe which is horizontally fitted across a wall. Now water jet is flowing through it,…
-
Maxwell Boltzmann distribution for a classical ideal gas
i. We assume a dilute gas which is enclosed by a thermally insulated container on all sides. Dilute gas in a thermally insulated container: Dilute means concentration of gas molecules is low. Insulated implies there is no reasonable flow of heat energy across the walls of the container. ii. Each molecule is assumed to be a…