M Dash Foundation: C Cube Learning

Ampere’s law application: infinite surface current, diagram. An infinite sheet of current in xy plane with Amperian loop. We like to determine its magnetic field by Ampere's Law.

Example 5.7; Application of Ampere’s law.

The following problem is an interesting application of Ampere’s law apart from usual applications found in honors syllabus (eg infinite straight conductor, Solenoid and Torroid). This is to be found in the excellent book by Griffith on Electrodynamics. (Example 5.7 from 3rd edition of Griffith Electrodynamics).

Applying Ampere's law to find the magnetic field due to an infinite surface current.
Applying Ampere’s law to find the magnetic field due to an infinite surface current.

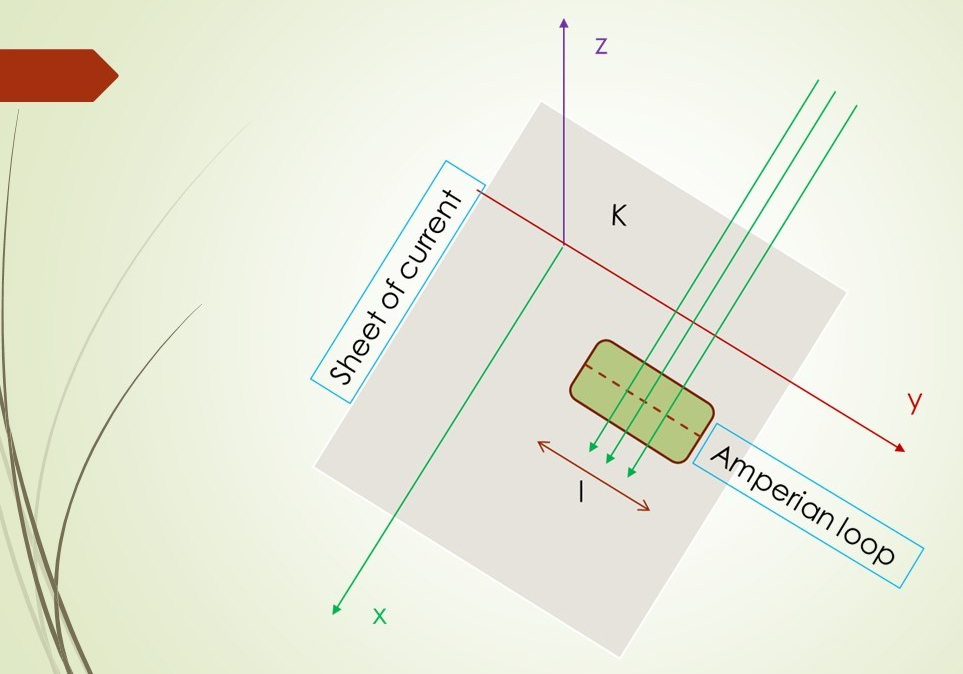
Lets first visualize the problem. This will help us solve the problem. We chose a Cartesian coordinate system as shown. Our infinite surface current is a sheet that is concurrent with the XY-plane. We also show the Ampere-loop which is a rectangle of length l parallel to the y-axis. This loop is half above the XY-plane and half below.

Ampere’s law application: infinite surface current, diagram. An infinite sheet of current in xy plane with Amperian loop. We like to determine its magnetic field by Ampere's Law.
Ampere’s law application: infinite surface current, diagram. An infinite sheet of current in xy plane with Amperian loop. We like to determine its magnetic field by Ampere’s Law.

Lets first of all find out the direction of the magnetic field due to the given current. The magnetic field can neither have a x-component nor have a z-component. The magnetic field is directed along y-axis only.

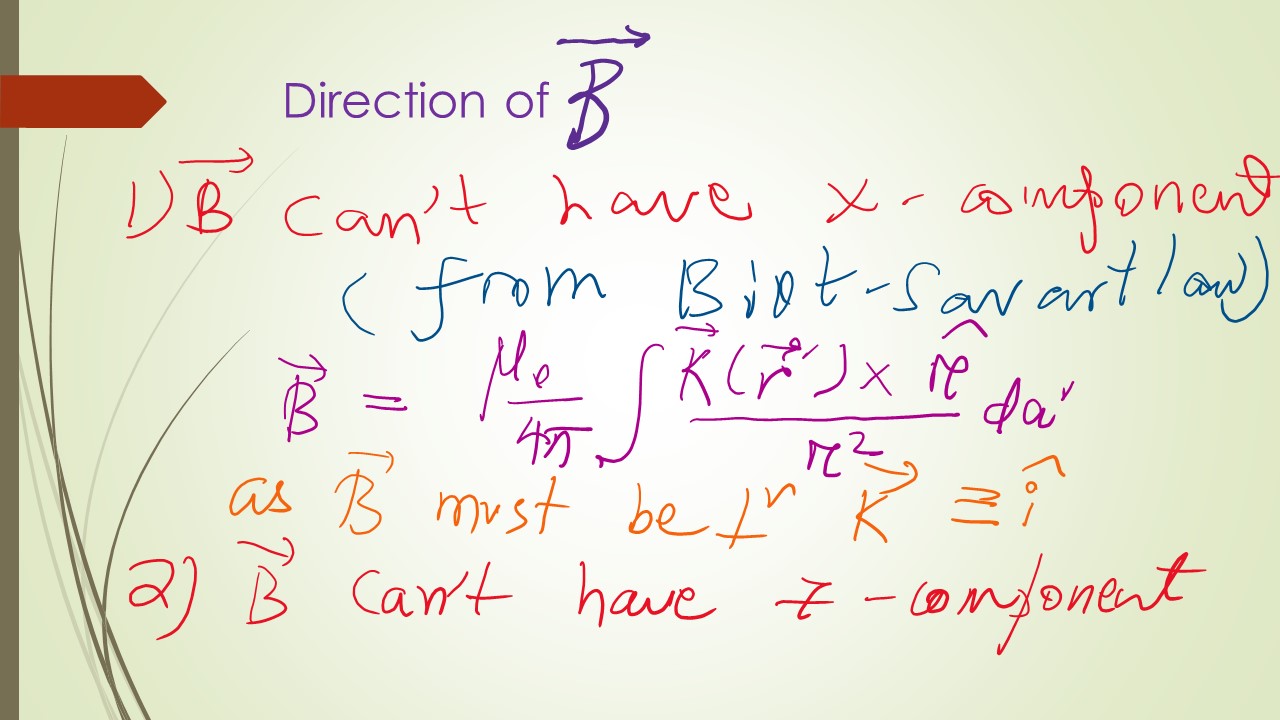
Direction of the field can't be along X-axis. Its inferred from the Biot-Savart law.
Direction of the field can’t be along X-axis. Its inferred from the Biot-Savart law.
Direction of the field can't be along Z-axis. This is from symmetry and Biot Savart law.
Direction of the field can’t be along Z-axis. This is from symmetry.
Direction of the field can't be along Z-axis. This is an alternate explanation from Biot Savart law.
Direction of the field can’t be along Z-axis. This is an alternate explanation from Biot-Savart law and symmetry.
Magnitude of the field can be evaluated by using symmetry of the situation and the solution as determined by Ampere's law. The field is directed both along +Y and -Y axes in different regions of space.
Magnitude of the field can be evaluated by using symmetry of the situation and the solution as determined by Ampere’s law. The field is directed both along +Y and -Y axes in different regions of space.

How did we know the direction of field for regions above and below the sheet of current? You can check with right-hand thumb rule for direction of current and direction of field. As simple as Mama’s instant snacks technique.

PS: erratum; read fillament as filament.

Posted

in

, , , , , , ,

by

Invariance, MDASHF i@M

Tags:

, , ,

Comments

One response to “Example 5.7; Application of Ampere’s law.”

  1. Problem 5.13 Application of Ampere’s Law – M Dash Foundation Avatar
    Problem 5.13 Application of Ampere’s Law – M Dash Foundation

    […] ( Infinite uniform surface current ) See that application of Ampere’s law first? […]

    Like

    Reply

Leave a comment