Category: Lectures & Presentations
-
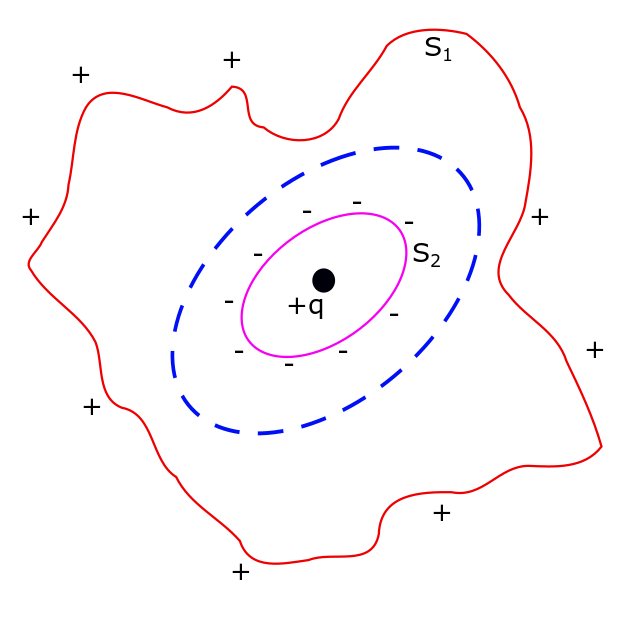
Conductors in Electrostatic Field, Lecture 13.
Conductors are materials which have at-least one electron per atom, that are free to move within the material. These are known as free or conduction electrons. There are no explanation in classical mechanics as to why there are free electrons in some materials. But these occurrences are well explained by quantum mechanics. According to quantum…
-
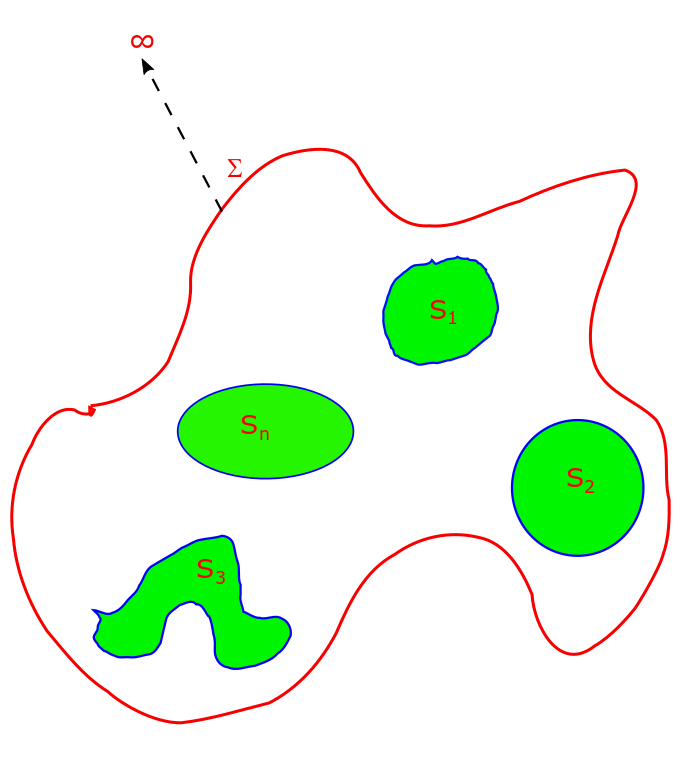
Uniqueness Theorem in Electrostatics, Lecture 12.
The uniqueness theorem can be stated as the following: “To every boundary value condition there exists a unique solution to the Laplace equation. Two solutions of Laplace equation that satisfy the same boundary value condition are (i) same for Dirichlet Boundary Value Condition and (ii) differ by an additive constant for Neumann Boundary Value Condition.
-
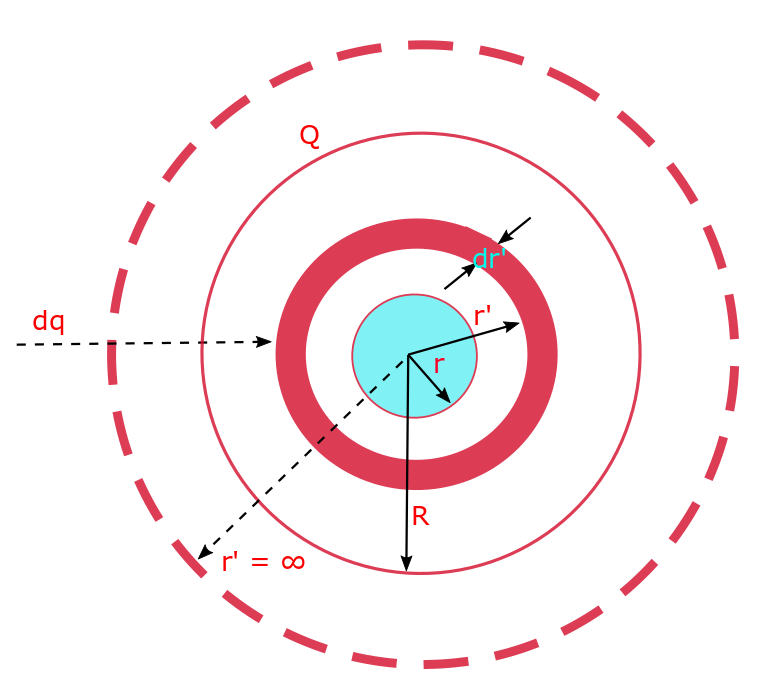
Electrostatic Potential Energy Of Different Charge Configurations. Lecture-10, 11.
We assume the charges to be located infinitely away from each other, initially. The charges interact among each other electrically when they come closer together, by the dint of Coulomb’s force. This gives rise to an electrostatic force between each pair of charge. When the charges come closer we have to perform work against the…
-
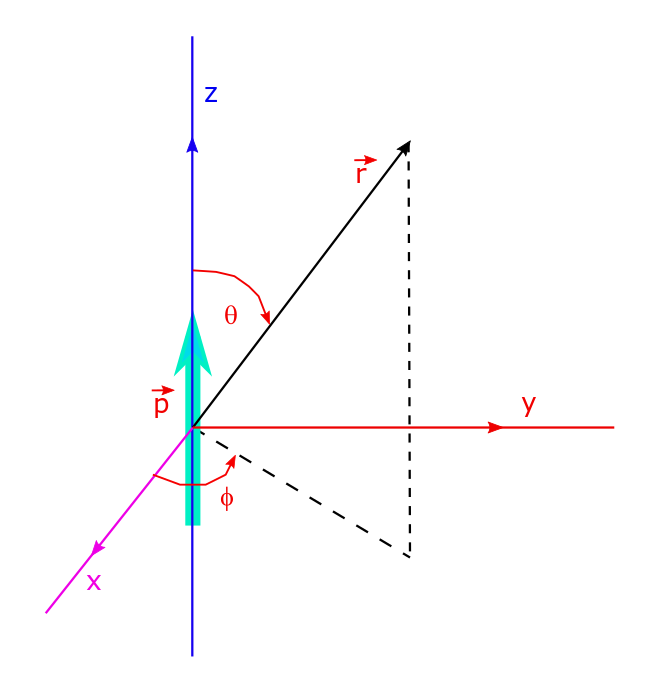
Electric Dipole: Potential And Electric Field Due To Dipole, Lecture-9.
An electric dipole is a system of two equal and oppositely signed charges +q and -q separated by a distance d. Atomic phenomena can often be modelled in terms of dipoles, so its important to study the dipole in detail. The electrostatic potential for such an arrangement (i.e. a dipole) can easily be written; Its…