Category: status
-
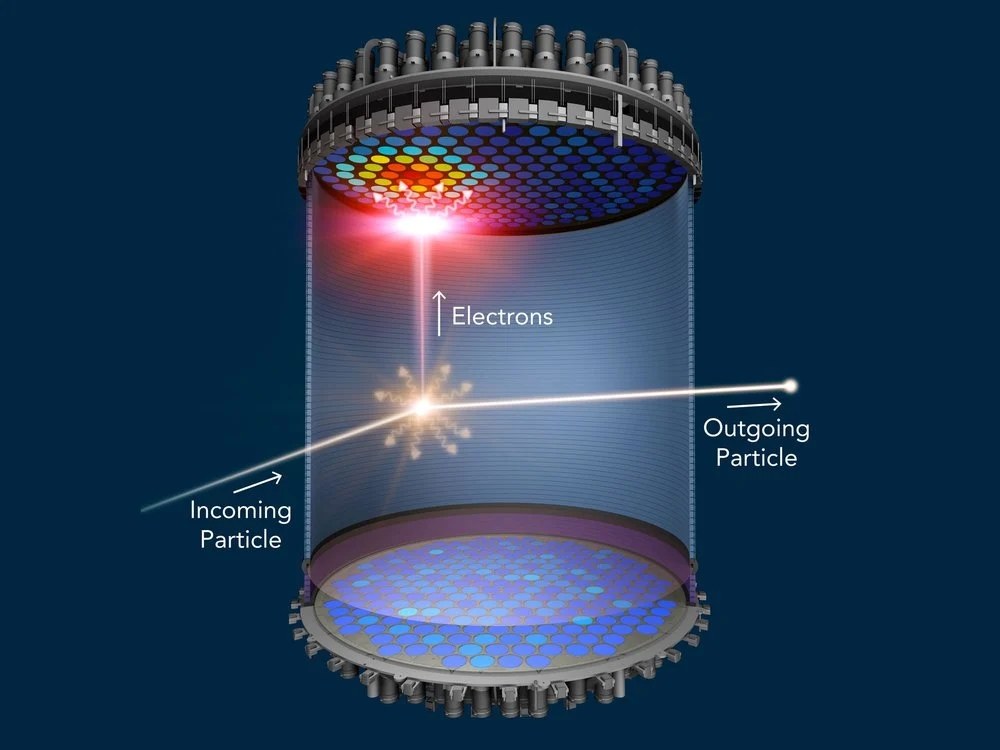
Physics interests me, what are my options?
Hi, I am Rithwik Mohanty and I currently go to Shelton High School. I possess a profound passion for the field of physics. More specifically I am interested in the modern aspects of physics. For example, some things that interest me are the search for dark matter and particle physics. I like to keep up…
-
Patriarchy
Most people out there would misunderstand the word patriarchy. They take it to mean: fatherly-rule or “through rule of the son from the father”. In-fact more than 200 years ago they constructed a new word matriarchy to counter this “sexism”. This new word meant passing of rights through mother’s side. While societies have been greatly…
-
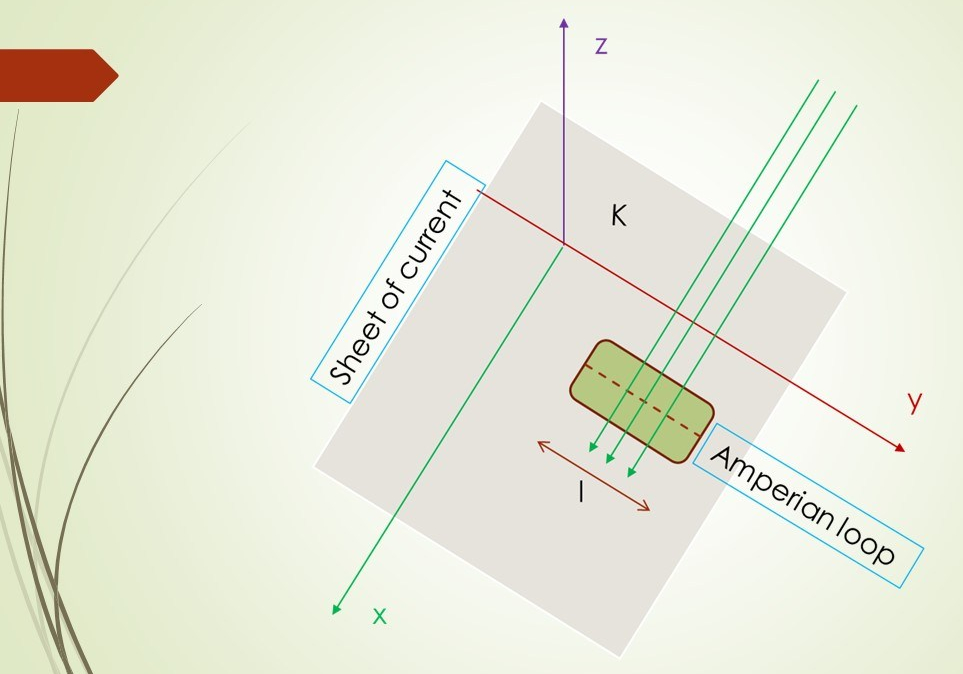
Example 5.7; Application of Ampere’s law.
The following problem is an interesting application of Ampere’s law apart from usual applications found in honors syllabus (eg infinite straight conductor, Solenoid and Torroid). This is to be found the excellent book by Griffith on Electrodynamics. Find the magnetic field of an infinite uniform surface current K (vect) = K i-cap, flowing over the…
-
Why light would curve under gravity?
Everyone was thinking in terms of physics (i.e. force). Einstein knew one part of that is maths, pure maths. Force is physics because of mass. But acceleration is geometry, its the shape of your trajectory and its maths. Imagine a pipe which is horizontally fitted across a wall. Now water jet is flowing through it,…
-

User experience @ M DASH F dot ORG — optimization issues.
I was doing some research on optimization of my website. This is what I found. Good news: My website is optimized for mobile devices, 15% better than some of the best blogs around the world. That means if you have been accessing my websites on your mobiles, you have been happy about your loading experience.…