M Dash Foundation: C Cube Learning

Tag: Poisson equation

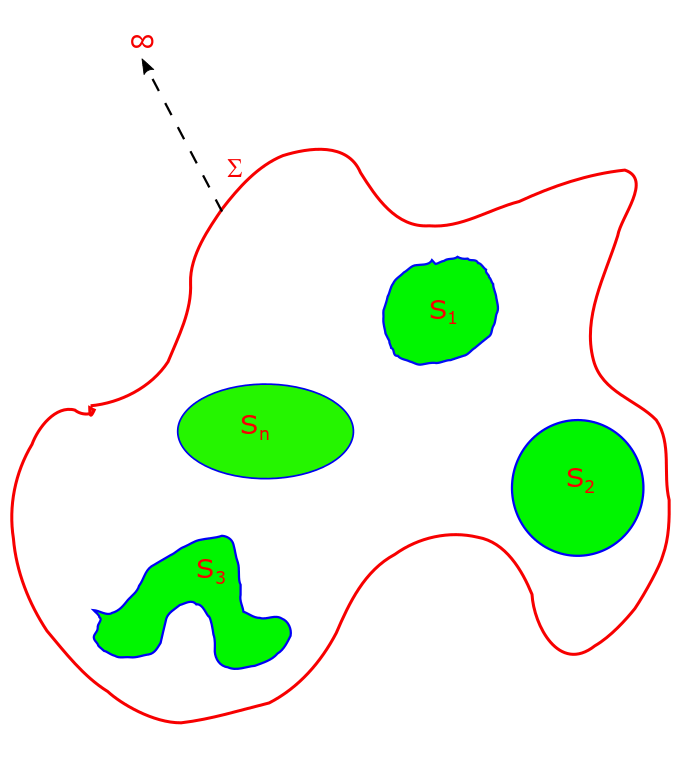
  • Uniqueness Theorem in Electrostatics, Lecture 12.

    Uniqueness Theorem in Electrostatics, Lecture 12.

    The uniqueness theorem can be stated as the following: “To every boundary value condition there exists a unique solution to the Laplace equation. Two solutions of Laplace equation that satisfy the same boundary value condition are (i) same for Dirichlet Boundary Value Condition and (ii) differ by an additive constant for Neumann Boundary Value Condition.

  • Laplace And Poisson Equation, Lecture 5, 6, 7 And 8.

    Laplace And Poisson Equation, Lecture 5, 6, 7 And 8.

    We will discuss 4 lecture hours of Laplace and Poisson Equation, their spherical coordinate forms and applications , boundary value problems in both spherical and Cartesian systems, there are 7 problems that are discussed in all details apart from required derivations.

  • Barrier potential and width in a pn step junction, L-VI.

    Barrier potential and width in a pn step junction, L-VI.

    Today we will discuss about the depletion region in greater detail than before. We will derive a quantitative relation among barrier potential and its width which are created in the depletion region, as discussed before. We will also derive an expression for the electric field that is established due to this potential. Lets first recall…