Barrier potential and width in a pn step junction, L-VI.

Analog systems and applications, lecture — VI.

“Barrier potential and width in a pn step junction, L-VI.”

This article belongs to a series of lectures on analog electronics, the paper goes by the name “Analog Systems and Applications” for the physics honors degree class. All lectures of this series will be found here. This is the sixth lecture of this series. This particular lecture was delivered on 25th January 2018.

Today we will discuss about the depletion region in greater detail than before. We will derive a quantitative relation among barrier potential and its width which are created in the depletion region, as discussed before. We will also derive an expression for the electric field that is established due to this potential.

So far we have the following 5 lectures in this series. You might wanna have a look through them, before or after reading this, for greater connectivity and assimilation of ideas.

Semiconductors and charge carriers lecture-I
Semiconductors and charge carriers lecture-II
Conductivity and mobility in semiconductors lecture-III
PN junction diodes lecture-IV
Energy levels in semiconductors lecture-V

Lets first recall how electric field and electric potential are related to each other. Electric field is the negative potential gradient. Mathematically, in 1 dimension this is expressed by the following formula.

$\boxed{ E = -\frac{dV}{dx}}$ .

In 3 dimensions it can be written as $\vec{E} = -\vec{\nabla}V$ , as the field E is a is a 3-dimensional vector. For our purpose only 1-dimension is enough as we are concerned about the direction which is perpendicular to the contact surface known as pn junction, we denote this perpendicular direction as ‘x‘.

We also know the Gauss law in electrostatics which has an integral form: $\oint \vec{E} \cdot \vec{dS} = \frac{Q_{encl}}{\epsilon_0}$ . By using the Gauss divergence theorem (of vector calculus) the integral form of Gauss law can be written as: $\vec{\nabla} \cdot \vec{E} = \frac{\rho}{\epsilon_0}$ , which in 1-dimension would look like: $\boxed{ \frac{dE}{dx} = \frac{\rho}{\epsilon_0}}$ . I.e. we are differentiating the 1-dimensional electric field along x-axis and we assume that the ‘y‘ and ‘z‘ variations of the field are zero.

Lets us now use the definition of the electric field ( $E = -\frac{dV}{dx}$ ) in the differential form of Gauss law, this leads to a differential equation: $\boxed{\frac{d^2V}{dx^2} = -\frac{\rho}{\epsilon_0}}$ . ( — eqⁿ 1 )

In 3 dimensions this equation would look like: $\nabla^2 V = -\frac{\rho}{\epsilon_0}$ , and it is known as the Poisson’s equation; (— eqⁿ 1) is also Poisson’s equation but it is so in 1 dimension.

In a medium we have to replace ε₀ by ε, the permittivity of the medium, the Poisson’s equation becomes: $\frac{d^2V}{dx^2} = -\frac{\rho}{\epsilon}$ . Here as we have already noted, ‘x‘ is the perpendicular distance from the barrier junction.

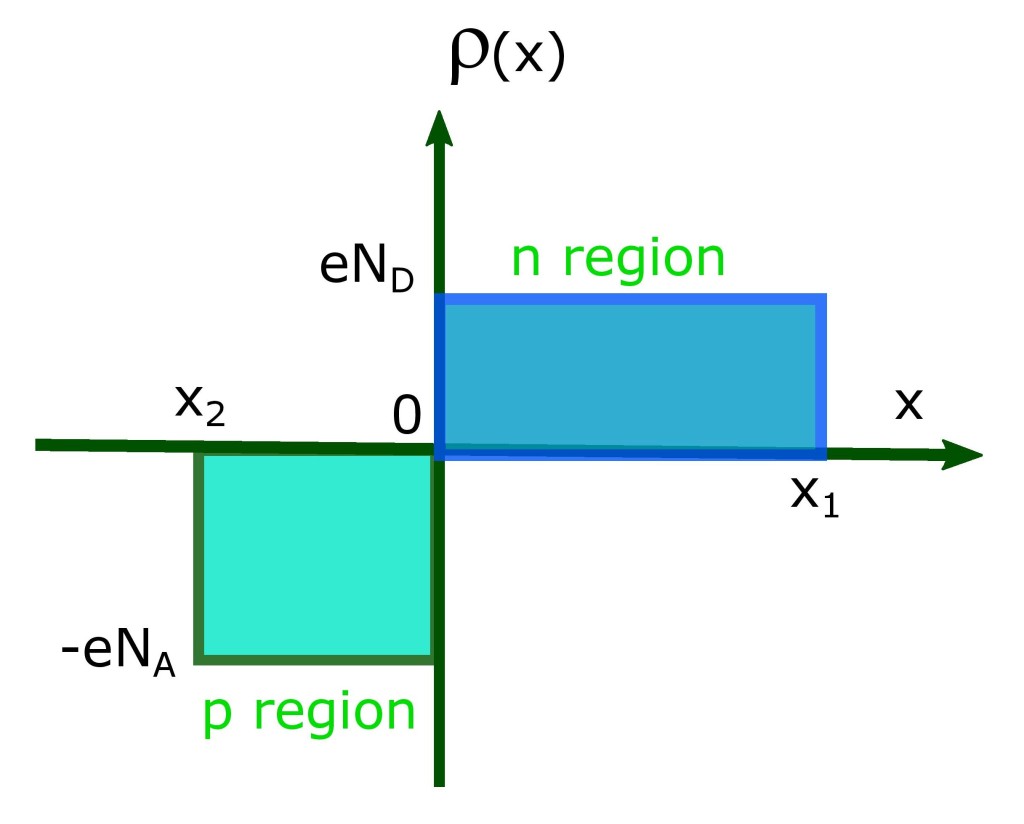
Let us now assume N_D to be the constant density of ionized ‘donor’ atoms, which extends to distance x₁, into n-region and N_A to be the constant density of ionized ‘acceptor’ atoms, which extends to distance -x₂ into p-region.

Let us also assume that the concentrations of electrons (n) and holes (p) are negligible in the “depletion region“. So, we have two equations for each region of the pn junction. One for the n-region and one for the p-region.

$\frac{d^2V}{dx^2} = -\frac{eN_D}{\epsilon}$ ( — eqⁿ 2 ) valid in the n-region (i.e. 0 < x <x₁) and

$\frac{d^2V}{dx^2} = \frac{eN_D}{\epsilon}$ ( — eqⁿ 3 ) valid in the p-region (i.e. -x₂ < x <0).

Electric field variation.

Let us now integrate ( eqⁿ 2 ) & ( eqⁿ 3 ). This gives us ( eqⁿ 4 ) in n-region and ( eqⁿ 5 ) in p-region.

$\frac{dV}{dx} = -\frac{eN_D}{\epsilon} x + C_1$ ( — eqⁿ 4 ) valid in the n-region and

$\frac{dV}{dx} = \frac{eN_A}{\epsilon} x + C_2$ ( — eqⁿ 5 ) valid in the n-region.

potential across depletion layer of a pn junction.

Potential is constant at the boundaries ( x = x₁ and x = x₂ ) as shown in the figure. i.e. $\frac{dV}{dx}|_{x=x_1} = 0,\,\,\,\,\, \frac{dV}{dx}|_{x=-x_2} = 0$ . This gives: $c_1=\frac{eN_D x_1 }{\epsilon}\,\,\,\,\, and \,\,\,\, c_2=\frac{eN_A x_2 }{\epsilon}$ .

Since “electric field is negative potential gradient” from ( — eqⁿ 4 ) we have: $E_n(x)=\frac{eN_D x}{\epsilon}-\frac{eN_D x_1 }{\epsilon} =\frac{eN_D (x-x_1) }{\epsilon}$ and from ( — eqⁿ 5 ) we have $E_p(x)=-\frac{eN_A (x+x_2) }{\epsilon}$ .

The field in each region increases as x approaches “zero” i.e. the junction. Electric field at the junction then is given by: $E_n(0)=-\frac{eN_D x_1 }{\epsilon}$ ( — eqⁿ 6 ) and $E_p(0)=-\frac{eN_A x_2}{\epsilon}$ . ( — eqⁿ 7 )

From “charge conservation” we have; $N_D x_1 = N_A x_2$ . ( — eqⁿ 8 )

Thus at the junction (x=0) $E_n(0) = E_p(0)=E_m$ . If the step junction is symmetric {i.e. x₁ = x₂ = x₀/2} at equilibrium; the value of maximum electric field, which exists at the junction, is given by: $\boxed{E_{0m}=\frac{eN_D x_0}{2\epsilon}}$ . ( — eqⁿ 9 )

‘0’ stands for equilibrium and x₀ ( = x₁ + x₂ ) is known as “width of the depletion region”.

Potential variation.

Let us integrate ( — eqⁿ 4 ) & ( — eqⁿ 5 ); and use the defining relation $V = - \int Edx$ for electric potential to get the electric potential from the above expressions for electric fields across the junction.

$V_n(x) = -\frac{eN_D}{2\epsilon}x^2 + \frac{eN_D x_1}{\epsilon}x + C_3$ in n-region (— eqⁿ 10) and

$V_p(x) = \frac{eN_A}{2\epsilon}x^2 + \frac{eN_A x_2}{\epsilon}x + C_4$ in p-region (— eqⁿ 11).

Now let is use the boundary conditions. The potential is zero where the depletion layer begins at the p-side (x=-x₂) and it is same as the builtin potential where depletion region ends on n-side (x=x₁). Mathematically: $V(x) = 0\,\,\,at\,\,\, x=-x_2$ and $V(x) = V_B\,\,\,at\,\,\, x=-x_1$ .

Then from the 2nd boundary condition above: $V_B = -\frac{eN_D {x_1}^2}{2\epsilon} + \frac{eN_D {x_1}^2}{\epsilon}x + C_3$ . This gives the value of the constant in the expression. We have: $C_3 = V_B -\frac{eN_D {x_1}^2}{2\epsilon}$ .

This gives us the expression for the potential in the entire n-region. $\boxed{V_n(x) = -\frac{eN_D}{\epsilon}[\frac{x^2}{2}+\frac{{x_1}^2}{2}-xx_1]+V_B}$ . (— eqⁿ 12)

From the 1st boundary condition above: $0 = \frac{eN_A {x_2}^2}{2\epsilon} - \frac{eN_A {x_2}^2}{\epsilon}x + C_4$ . This gives the value of the constant in the expression. We have: $C_4 = \frac{eN_A {x_2}^2}{2\epsilon}$ .

This gives us the expression for the potential in the entire p-region. $\boxed{V_p(x) = \frac{eN_A}{\epsilon}[\frac{x^2}{2}+\frac{{x_2}^2}{2}+xx_2]}$ . (— eqⁿ 13)

Junction potential and width of depletion layer.

The potential V must be continuous at the junction (x=0). This implies $V_n(0) = V_p(0)$ . Therefore: $-\frac{eN_D }{\epsilon}\frac{{x_1}^2}{2}+V_B = \frac{eN_A}{\epsilon}\frac{{x_2}^2}{2}$ . This gives us the value for V_B.

$V_B = \frac{eN_A}{\epsilon}\frac{{x_2}^2}{2}+\frac{eN_D }{\epsilon}\frac{{x_1}^2}{2}$ . But we have the expression: $N_D x_1 = N_A x_2$ for charge conservation and this leads to: $V_B = \frac{e}{2\epsilon}[1+ \frac{N_A}{N_D}]N_A {x_2}^2=\frac{e}{2\epsilon}[1+ \frac{N_D}{N_A}]N_D {x_1}^2$ .

Let us now solve for x₁ and x₂.

$x_1 = [\frac{2\epsilon N_A V_B}{e (N_A+N_D)N_D}]^{\frac{1}{2}}$ and $x_2 = [\frac{2\epsilon N_D V_B}{e (N_A+N_D)N_A}]^{\frac{1}{2}}$ .

This gives us the total depletion width or the asymmetric step junction width: $\boxed{W = x_0 = x_1 + x_2 = \frac{2\epsilon V_B (N_A+N_D)}{e N_AN_D}}$ .

For symmetric step junction: x₁ = x₂ = x₀/2 and N_A = N_D = N. Then: $\boxed{W = x_0 = \bigg(\frac{4\epsilon V_B}{e N}\bigg)^\frac{1}{2}}$ .

For one sided step-junction, one side of pn junction is heavily doped, eg, if p-region is heavily doped then x₂ << x₁ as N_A >> N_D. Then; $\boxed{W = x_0 = x_1 = \bigg(\frac{2\epsilon V_B}{e N_D}\bigg)^\frac{1}{2}}$ .

If donors on n-side are all ionized, electron conductivity σ_n in terms of its mobility is given by: $\sigma_n = \mu_n e N_D$ .

This implies: $\boxed{W = x_0 \simeq \bigg(\frac{2\epsilon \mu_nV_B}{\sigma_n}\bigg)^\frac{1}{2}}$ .

Peak electric field can be obtained from the plot of electric field shown earlier (triangles). Area of triangle (V_B) is half the base (x₀) times height (E_m) So, $\boxed{E_m=\frac{2V_B}{x_0}}$ .

2 thoughts

Pingback: Current and resistance in pn junction diodes, L-VII. – M Dash Foundation: C Cube Learning
Pingback: Bipolar Junction Transistors (BJT), Lecture-XV and XVI. – M Dash Foundation: C Cube Learning

M Dash Foundation: C Cube Learning

Invariance: A journal with a difference, where mind meets aspiration

Barrier potential and width in a pn step junction, L-VI.