Fermat’s Principle, a lecture in optics

Optics series, lecture — III

This lecture was delivered on 30th January 2017

( All other lectures in the optics series ) Access other available lectures in the optics series

“Fermat’s principle of least time in geometrical optics”

Geometric Optics: When the size of objects that a wave of light interacts with are large compared to the wavelength of light λ, λ can be neglected for practical purposes and the light waves behave like rays of light. Rays of light are geometric line segments from one point of incidence of light to another. Study of optics under the limit of negligible wavelength λ → 0, is called geometric optics.

Geometric optics can be studied using Fermat’s principle, much like motion of objects in the realm of classical mechanics are studied using Newton’s laws of motion. To know the basic grounding of Fermat’s principle follow the links to read two articles which expound the subject matter of Fermat’s principle, article 1 — a detailed, historical and kind of long article, and article 2 — a conceptual but a short article.

( Article 1: Optical path ) Read further on Optical path and Fermat’s principle

( Article 2: Inherent ability and action principle ) Read action principle from a concise conceptual view point

Before Fermat, Hero of Alexandria, who lived sometime between 150 BC and 250 AD explained reflection of light. ( Read the more extensive history in the already linked article, article 1 above ) His formulation is stated as principle of shortest path.

Since reflection occurs in only one medium ( homogeneous medium ) light indeed travels a geometric shortest path; this is the straight line path between any two points — or coordinate of the ray. For homogeneous medium optical path and physical and geometrical path are merely either proportional to each other or equal.

In the modern times Fermat reformulated Hero’s principle of shortest path — to its equivalent form of shortest optical path. This entailed the principle to be applicable to both reflection and refraction and any other possible optical phenomena which could be explained by virtue of Fermat’s principle in general.

In its original — shortest path form the principle could not explain refraction, because the latter involves traversal of light rays in in-homogeneous media, that is different media are traversed at different speeds and optical path and geometric or physical path are no more equivalents. We will soon see this in detail.

The new formulation of Fermat which is based on improvement of the earlier Hero’s principle for reflection is called as Fermat’s principle of least time. It states that “a ray of light travels through those coordinates of the ray in a given system of media of varying refractive indices for which the amount of time taken is least .”

This can successfully explain both reflection and refraction. But it can still be generalized and the modern form is in terms of the shortest optical path which is different from how it was originally formulated. Before we study the modern form lets discuss its original form.

According to Fermat “the ray of light will correspond to that path for which time taken is an extremum in comparison to nearby paths” Mathematically extremum implies time for a particular path can be minimum, maximum or stationary for a given neighborhood of paths.

If n (x, y, z) is the refractive index as a function of path or position (x, y, z) then; $\boxed{t=\frac{ds}{v}=\frac{ds}{cn^{-1}}=\frac{n\,ds}{c}}$ , where ds is an element of the path traversed by the ray of light so that n is the refractive index.

Fermat's Principle of least time: two neighboring paths for light, which will light chose? Photo Credit: mdashf.org — **Fermat’s Principle of least time**: two neighboring paths for light, which will light chose? **Photo Credit**: mdashf.org

Lets consider two paths between the coordinates A and B of the ray of light, as shown above, one that goes via C and the other that goes via C’. Then the total time taken for path ACB is:

$\boxed{time=\tau=\frac{1}{c}\,\Big(\sum_i n_i \,ds_i\Big) \,\,\,\,\,or\,\,\,\,\,\frac {1}{c}\,\bigg(\int\limits_{\substack{A\,C\,B}} n\,ds\bigg)}$

We define: $\int n\,ds$ or $\sum\limits_{\substack{i}} n_i \,ds_i$ as the optical path length or OPL. Then;

Fermat’s original principle: can be stated as; the actual path between two points taken by a ray of light is the one which is traversed in the least time”.
Modern or modified form: can be stated as; the actual path of ray of light between two points is the one for which the optical path length is stationary with respect to the variation of the path in its neighborhood.
Mathematically therefore: $\delta \int n\,ds =0 \,\,\,\,\,\,\,\,\,or\,\,\,\delta \,(\,OPL\,)=0$

Therefore for a homogeneous medium i.e. a medium where refractive index does not change with position, rays will always travel in straight lines. This corresponds to Hero’s law of reflection.

We have discussed in great detail why the Hero’s law is not sufficient to explain the idea of refraction , ( linked below ) since it involves multiple refractive indices to be stated for the given problem. We will thus resort to the modern formulation of Fermat’s principle to explain the law of reflection and refraction.

( Article 1: Optical path ) Read further on Optical path and Fermat’s principle

Law of reflection

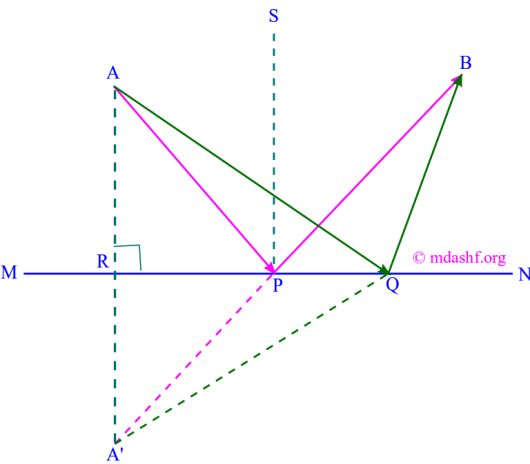
Consider a plane mirror MN.

Fermat's Principle of least time: Reflection by Fermat's principle Photo Credit: mdashf.org — **Fermat’s Principle of least time**: Reflection by Fermat’s principle **Photo Credit**: mdashf.org

Path of ray from A to B should have minimum optical length, lets say through P, from symmetry considerations. We have shown an alternative path — after suggestions from Donald Trump. Its shown as AQB. Whichever path it is, it must have a minimum optical path if Fermat were right. The whole path of light is in a homogeneous medium.

This means minimizing optical path is same as optimizing the geometric path shown here. That means for path APB, AP + PB is minimum in comparison eg to path AQB. ( i.e. AP + PB ≤ AQ + QB for all Q )

Let us drop a perpendicular from A to MN so that A’R = AR. But AP = A’P, AQ = A’Q. AQB is an alternative path. We have to now minimize A’PB ( in lieu of APB ). P must be on straight line A’B. Thus A, A’, P and B are all on the same plane as is normal PS. Geometric considerations lead to equality of the angles ∠APS and ∠SPB.

For minimum optical path length angle of incidence i ( ∠APS ), angle of reflection r ( ∠SPB ) are equal and incident ray, reflected ray and normal are on the same plane. This is the law of reflection and Fermat’s principle leads to this.

Law of refraction

Now let us consider a refracting surface PQ which interfaces medium with refractive index n₂ to a medium of refractive index n₁. Let the actual path of the ray be ARB. For minimum optical path length incident ray, refracted ray and normal to interface surface must all be in same plane.

Fermat's Principle of least time: refraction by Fermat's principle of least time Photo Credit: mdashf.org — **Fermat’s Principle of least time**: refraction by Fermat’s principle of least time **Photo Credit**: mdashf.org

Lets drop perpendicular AM and BN from A and B to the interface surface PQ. We denote length of AM, BN, MR, RN and MN by AM = h₁, BN = h₂, MR = x, RN = L – x and MN = L = constant.

Lets calculate the optical path length. OPL = L_op = n₁( AR ) + n₂( RB ) = $n_1\,\sqrt{x\,^2+(h_1)\,^2}+n_2\sqrt{(L-x)^2+(h_2)\,^2}$ .

Since $\frac{d\,(L_{\,op})}{dt}=0$ so, $\frac{n_1\,x}{\sqrt{x^2+(\,h_1\,)\,^2}}-\frac{n_2\,(\,L-x\,)}{\sqrt{(\,L-x\,)\,^2+(\,h_2\,)\,^2}}=0$ .
But $\sin\,(\,\theta_1\,)=\frac{x}{\sqrt{x^2+(\,h_1\,)\,^2}}$ and $\sin\,(\,\theta_2\,)=\frac{L-x}{\sqrt{(\,L-x\,)^2+(\,h_2\,)\,^2}}$ .
So we have: $n_1\,\sin\,(\,\theta_1\,)=n_2\,\sin\,(\,\theta_2\,)$ . Thus we have the Snell’s law of refraction from Fermat’s principle.