Harmonic plane waves

Optics Series, lecture – VIII
This lecture ( 1.5 hours ) was delivered on 13th February 2017 to honors students

( all optics series lectures ) go to other available optics lectures

“Harmonic plane waves”

In our last lecture ( lecture — VII ) we began by discussing what are electromagnetic waves. We also discussed in good detail what are harmonic waves. Harmonic waves are those waves whose wave – profile is either sine, cosine or in general a combination of both sine and cosine. You can learn more about what is wave profile and how to transform a wave profile into a traveling wave in the following lecture.

( previous lecture, lecture — VII ) read more about waves, especially electromagnetic waves

( wave profile and travelling wave ) learn more about wave profile and travelling wave

A wave profile, wave form or wave shape is simply a spatial snapshot view of a more general moving wave, at a suitable time. We have also discussed what is a plane wave. We studied the interesting phenomena of interference between two plane waves in the context of our harmonic plane waves. We assumed that our harmonic plane waves are also monochromatic waves, that is they have the same same wavelength.

These waves traveling in a homogeneous media have a fixed frequency and as long as they are in free – space their speed remains unaltered at the speed of light value c = 3 × 10⁸ m/s.

A plane wave is a traveling wave where the wave fronts are planar points with equal phases anywhere on the plane. In a similar manner a spherical wave front is the locus of uniform phase over a spherical configuration and a cylindrical wave front would be a traveling wave where the locus of uniform phase is nothing but a cylindrical surface.

In one of the lecture we have discussed in much detail what are spherical waves. Cylindrical waves have been left to the advanced and willing students to work out by themselves. If time permits sometime in the future we can fall back and make a case for cylindrical wave fronts as well. But I make no promises at this point.

( Spherical waves, lecture — X ) Read about the spherical waves

Note that the waves are simply a motion of the phase points and therefore waves are a function of the space ( or location ) and time instant by which they are described. A phase is nothing but the angular argument of the wave described in terms of harmonic functions. Since harmonic functions ( another name for sinusoidal functions ) are periodic functions and trigonometric functions have a certain periodicity in terms of angular values, a phase represents the angular value ( or argument ) of these functions.

Plane Waves

Let us begin studying the plane waves in detail. Here are some of its features.

1. plane wave: a plane wave is the simplest example of a 3-dimensional wave.
2. why named so: plane waves are so called, because plane wave have wave fronts that are planar in shape. A wave – front is a locus of points on which the phase of the wave is same. Its a surface of wave – disturbances which move together, at the same speed.
3. simplest example: optical devices are often tuned to produce plane waves. This necessitates the study of plane waves as base examples, where more complicated features can be assigned when they become pertinent.

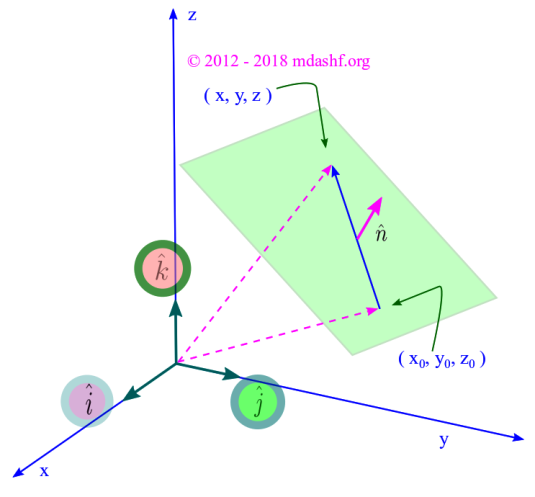
Wave fronts are always perpendicular to the direction of wave propagation. We need to find the mathematical expression for a plane which is perpendicular to a given vector $\vec{k}$ and passes through some point given by the constant position vector $\vec{r}_0\equiv \,(\,x_0,\,y_0,\,z_0\,)$ .

Let us remember that $\vec{k}$ is the wave propagation vector, hence the wave disturbance moves along the vector $\vec{k}$ . We have the position vector $\vec{r}$ which varies along from one space point to another. As a result we have the following: $\vec{r}\equiv ( x,\,y,\,z)$ , so $\vec{r}-\vec{r_0}\equiv (x-x_0)\,\hat{i}+(y-y_0)\,\hat{j}+(z-z_0)\,\hat{k}$ .

$\boxed{(\vec{r}-\vec{r}_0)\cdot \hat{k}=0}$ .

Let us draw a suitable diagram to understand the above scenario.

Harmonic wave: Plane wave front of a harmonic wave. Photo Credit: mdashf.org — **Harmonic plane waves**: Plane wave front of a harmonic wave. **Photo Credit**: mdashf.org

Equation for the wave front: Let us rewrite the above equation by recognizing that: $\vec{k}=k_x \,\hat{i}+k_y \,\hat{j}+ k_z \,\hat{k}$ which leads to: $k_x \,(x-x_0)+k_y\, (y-y_0)+ k_z \,(z-z_0)=0$ so that: $k_x\, x+k_y \,y+ k_z \,z=a$ where $a = k_x\, x_0+k_y \,y_0+ k_z\, z_0=constant$ . We see that any plane perpendicular to the wave propagation direction $\vec{k}$ passing through $\vec{r}_0\equiv \,(\,x_0,\,y_0,\,z_0\,)$ is given by: $\boxed{\vec{k}\cdot \vec{r}=constant=a}$ and each point in this plane has the same projection on $\vec{k}$ ; the wave propagation direction.

Let us now consider the harmonic or sinusoidal waves as we hinted at the beginning of the lecture. Our goal is to construct a set of planes over which ψ ( r ) varies in space in a harmonic or sinusoidal manner.

The function ψ ( r ) is called the wave function and according to our choice it is sinusoidal — that is, it has sine or cosine variation or a combination thereof, hence it has the following form: $\psi\, (\,\vec{r}\,) = A\, \sin\, (\,\vec{k}\cdot\vec{r}\,)$ , $\psi\, (\,\vec{r}\,) = A\, \cos\, (\,\vec{k}\cdot \vec{r}\,)$ or in general: $\psi \,(\,\vec{r}\,) = A\, e^{\,\,i\,\vec{k}\, \cdot\, \vec{r}}$ . As we saw above ψ ( r ) is constant over any plane defined by: $\boxed{\vec{k}\cdot \vec{r} = constant = a}$ .

Wavelength and wave number, a result of wave’s spatial periodicity: The wave – function ψ ( r ) repeats itself in space after a displacement of λ, in the direction of vector $\vec{k}$ . λ is called as the wavelength of the wave. According to this definition of wavelength λ, we have: $\psi \,(\,\vec{r}\,) =\psi \,(\,\vec{r}+\frac{\lambda \,\vec{k}}{k}\,)$ , note that; $\hat{k}\neq \frac{\vec{k}}{k}$ we can instead use $\hat{n} \equiv \frac{\vec{k}}{k}$ . So k is the magnitude of the vector $\vec{k}$ . The magnitude is known as wave number or propagation number and the vector $\vec{k}$ is known as the propagation vector or wave vector. Do not confuse between the unit vector along z-axis, denoted as k-cap and the unit vector along vector $\vec{k}$ , the propagation vector, which as a good measure, we can denote rather by n-cap. For a plane harmonic wave therefore the periodicity condition that we just introduced in terms of wavelength λ, is given by: $\boxed{A\, e^{\,i\,\vec{k}\,\cdot\,\vec{r}} = A\,e^{\,i\,\vec{k}\,\cdot\,(\,\vec{r}\,+\,\lambda \, \frac{\vec{k}}{k} \,)} =A\,e^{\,i\,\vec{k}\,\cdot\,\vec{r}}e^{\,i\,\lambda \,k}}$ . This means: $e^{\,i\,\lambda\, k}=1 = e^{\,i\,2\,\pi}$ so, $\lambda\, k= 2\pi$ or $\boxed{k = \frac{2\pi}{\lambda}}$ .

Let us display the wave – fronts of the harmonic plane waves by a diagram.

Harmonic wave: Plane wave fronts of harmonic wave, travelling along direction of k vector. Photo Credit: mdashf.org — **Harmonic plane waves**: Plane wave fronts of harmonic wave, travelling along direction of k vector. **Photo Credit**: mdashf.org

Our constructed plane harmonic wave – fronts are such that at any fixed point in space r is constant and this means the phase is constant as is the wave function ψ ( r ). In other words planes defined by: $\vec{k}\cdot \vec{r}=constant=a$ are not yet moving. The planes inherit motion when the wave function varies as a function of time, that is ψ ( r ) becomes a time dependent function.

We introduce a time dependence into our harmonic wave function to convert them into traveling waves. The method is discussed in this lecture. So we have now a travelling wave given by: $\psi \,(\vec{r},\,t) = A \, e ^{\,i\,(\,\vec{k} \,\cdot \,\vec{r} \,\,\mp\, \,\omega \,t\,)}$ where A, ω and k are constant.

We see that each ( space, time ) point is associated with a phase corresponding to the value of the wave – function at this point. We have seen that surfaces that include all points of equal phase are known as wave – fronts. Any wave front will have the same value of the wave function at all points on it if the amplitude A is independent of points on the wave front.

That is amplitude A is uniform over the wave – front. Such waves are known as homogeneous waves. We would not be dealing with in-homogeneous waves at the moment. So for us, the amplitude would be independent of various points on the wave – front.

Wave velocity

The phase of a plane harmonic wave moves at certain speed, it gives us the propagation velocity of the wave front and is known as phase velocity. Thus wave velocity is the phase velocity, when there is only a single wavelength wave ( monochromatic wave ) is passing through a homogeneous medium. This will change if the wave consists of many different wavelengths ( or multiple frequencies of waves).

In such a case the speed of the wave depends on wavelength or frequency of the wave, which are now multiple in number, either discrete or continuous. Thus the frequency ω is a function of wave number k or equivalently wavelength λ. Such interdependence of the speed, frequency, wavelength or wave number of the wave, expressed mathematically ( eg ω = ω ( k ) ) are known as dispersion relations.

Accordingly wave velocity can be of two types, for monochromatic components, its the phase velocity and for poly-chromatic waves, its the group velocity, where group velocity is the combined value of different phase velocities.

Wave velocity of harmonic plane wave: Let us find out the phase velocity of our monochromatic plane harmonic wave given as: $\psi \,(\vec{r},\,t) = A \, e ^{\,i\,(\,\vec{k} \,\cdot \,\vec{r} \,\,\mp\, \,\omega \,t\,)}$ . When $\vec{r}$ has a component r_k along vector $\vec{k}$ we can write: $\psi \,(\,\vec{r},\,t\,) = \psi\,(\,r_k + dr_k, \, t+dt\,)=\psi\,(\,r_k, \,t\,)$ because the wave disturbance is constant on the wave front which moved a distance dr_k in time dt. In terms of the harmonic wave function we had conjured above: $A \, e ^{\,i\,(\,\vec{k} \,\cdot\, \vec{r}\, \,\mp\, \,\omega\, t\,)}=A \, e ^{\,i\,(\,k\,r_k \,+ \,k\,dr_k \,\mp\, \omega \,t \,\mp\, \omega \,dt \,)}= A \, e ^{\,i\,(\,k\,r_k \,\mp\, \omega \,t)}$ . This gives us: k × dr_k = ± ω × dt. Since dr_k is the distance moved by the wave in a time dt we have the wave velocity v given by: $\boxed{\frac{dr_k}{dt}=\pm\,\, \frac{\omega}{k}=\, \pm\, v}$ .

Forms of harmonic plane wave

Let two waves ψ₁ and ψ₂ move along two different directions. Let them have the same wavelength λ so that the wave numbers ( magnitude of wave vectors ) are the same, given by k₁= k₂= k = 2π / λ. Also let ψ₁move along z-axis — that is, propagation direction is along vector k-cap ( $\hat{n}_1 = \hat{k}$ ). Let ψ₂move along vector $\vec{k}_2 \,(\,=\,k_2\hat{k}_2=k\hat{n}_2)$ so that this vector makes angle θ with z-axis and lies in the y – z plane.

Forms of harmonic plane wave: From this we have: $\hat{n}=\frac{\vec{k}_1}{k_1}=\hat{k}$ , $\vec{k}_1\cdot\vec{r}=k_z = \frac{2\pi}{\lambda}z$ , $\vec{k}_2\cdot\vec{r}=k_z\,z + k_y\,y = (\,k\,\cos\,\theta\,)\, z + (\,k\,\sin\,\theta\,)\, y$ , $\psi_1 = A_1 \,cos \, \big(\frac{2\pi}{\lambda} z - \omega t\big)$ and $\psi_2 = A_2 \,\cos \, \big[ \frac{2\pi}{\lambda}\,(\, z \,\cos \,\theta + y \,\sin\,\theta \,)- \omega \,t\big ]$ . Now let us write the plane harmonic wave in Cartesian coordinate system; $\psi\,(\,x,\,y,\,z,\,t\,)=A\,e^{\,i\,(\,k_x\, x \,+\, k_y \,y \,+\, k_z\, z \,\,\mp \,\, \omega \,t\,)}$ or $\boxed{\psi\,(\,x,\,y,\,z,\,t\,)= A\,e^{\,i\,[\,k\, ( \,\alpha \,x\, + \,\beta\, y\, +\, \gamma \,z\,)\,\mp \, \omega\, t\,]}}$ where α, β and γ are the direction cosines of the vector $\vec{k}$ . i.e. $\vec{k}=k_x\, \hat{i} + k_y \,\hat{j} + k_z\,\hat{k},\,|\vec{k}|=k=\sqrt { (k_x )\,^2 + (k_y) \,^2 + (k_z) \,^2 }$ and $\alpha = \frac{k_x}{k},\,\beta= \frac{k_y}{k},\,\gamma= \frac{k_z}{k},\, \alpha^2 + \beta ^2 + \gamma ^2 = 1$ .