Conductors in Electrostatic Field, Lecture 13.

Lectures on Electricity and Magnetism — new series of lectures – EML – 13.

All articles in this series will be found here. Click on link to left or search for menu “E AND M BASICS” on top.

Conductors in Electrostatic Field

What Are Conductors?

Conductors are materials which have at-least one electron per atom, that are free to move within the material. These are known as free or conduction electrons. There are no explanations in classical mechanics as to why there are free electrons in some materials. But these occurrences are well explained by quantum mechanics.

According to quantum mechanics electrons are described by stationary state wave functions (eigenfunctions) which are characterized by particular values of energy (energy eigenvalues). When the binding energy of the electron (with its parent atom/nucleus) is very small, it can drift away from its parent nucleus if an individual atom is considered.

What happens when there are a sea of atoms? The electrons with high binding energy can’t move across one nucleus but the ones with small binding energy can wander in the vicinity of multiple nuclei. Their wavefunction now spreads out across a large distance of the material sample. Such wavefunctions are now called as Bloch waves after the physicist Felix Bloch. Classically this manifests as free electrons.

Conductors have an abundance of free electrons. Why then these electrons do not come out of the conductors? When free electrons are located inside of the conductor they are surrounded by nuclei on all sides and there is no net force on these electrons. When the electrons arrive at the surface a net positive charge develops which pulls the electrons at the surface to the inside. The positive charges in this case are known as “image charges”.

The free electrons at the surface can be imparted a large amount of energy e.g. by heating the conductors. As a consequence the free electrons at the surface can break away from the conductors. This is known as thermionic emission.

So there are free and bound electrons inside of a conductor, how do they interact with an externally applied field? The bound charges behave as they would behave in dielectrics, where they are not free. But they they develop electric dipole moments and cancel some of the electric field, applied externally. You can learn the basics of electric dipole moments here in lecture EML-9.

The free electrons on the other hand move to the surface of the conductors and continue to rearrange themselves, but they can’t eject from the surface under normal circumstances. They create an electric field of their own. They come to rest on the surface when their electric field balances out the field of the external application. Under equilibrium conditions for a steady externally applied field there will be no net electric field on the body of the conductor. The external field and the one created by the surface charges cancel each other.

+ click to see more about this article

This article belongs to a group of lectures I intend to prepare for their online dissemination — these were delivered in a physical format, beginning with hand written notes that were delivered in a classroom full of students. This series is on Electricity and Magnetism and bears the name sake Electricity and Magnetism Lectures and the number of the lecture will be appended to the end to reflect the same. eg the current lecture will be named EML – 13. This lecture was delivered to honors students on 21st Feb 2017.

In the meanwhile if you can’t wait and you need some of these concepts at the earliest, here is a slide-share presentation I had made roughly 5 years ago that consists of “some of the things” an undergrad needs: Electricity and Magnetism slides. There are other slides on different topics at that account of mine on slideshare.net (such as; Introduction to Quantum Mechanics , and these are quite well received by the community for their usefulness).

Conductors Are Equipotential Surfaces

Since the body of the conductor has no electric field, the work done corresponding to any oath in the body is zero, so all the points on the conductor are now at the same potential, hence conductors are equipotential surfaces. Read more about the concept of electrostatic potential here in lecture EML-4. The electric fields on the surface are always perpendicular to the surface. Any motion of the surface charges produces tangential electric field, which vanishes when surface charges rearrange to keep only the perpendicular component of the field.

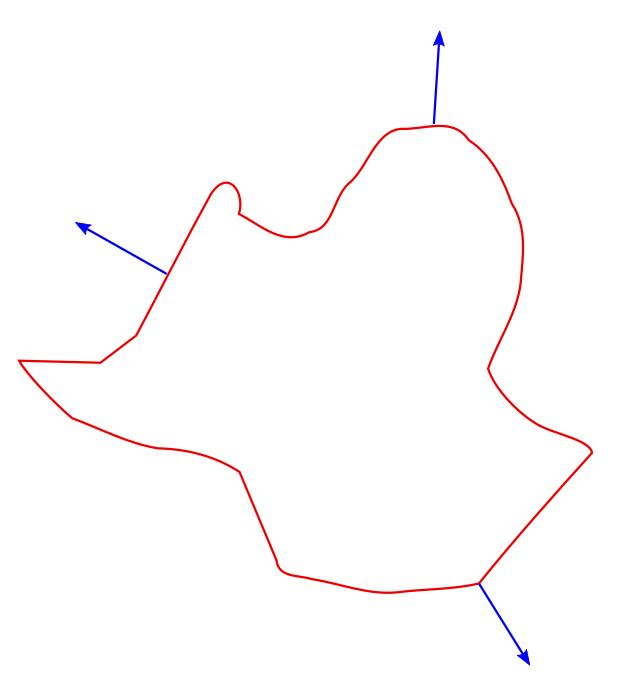
A conductor in an electrostatic field necessitates normal electric field to any point on the surface of the conductor. In the body of the conductor the field must be zero, potential therefore must be same everywhere.

Any net charge densities reside only on the surface and not on the inside of the conductor. If there is a cavity inside of the conductor, e.g. as shown in the diagram below, the surface of the cavity S₂ in the diagram will be at the same potential as that of the surface S₁. No work will be done in moving charges from S₁ to S₂ as there is no potential difference that exists between these surfaces. (as we already said because there is no electric field existing in the intermediate region. This corresponds to zero force, zero work done hence zero potential and zero potential energy).

A conductor with a cavity in an electrostatic field. The cavity can't have any electric field as does the body of the conductor. The cavity must have the same potential as the rest of the conductor body. — A conductor with a cavity in an electrostatic field. The cavity can’t have any electric field as does the body of the conductor. The cavity must have the same potential as the rest of the conductor body.

There will be no surface charges on S₂. If there are surface charges on S₂, the field lines can’t penetrate the conductor and all of it has to go to the cavity. Read more about electric field lines here in lecture EML-1.

Lets consider the following diagram that shows a flux line passing from point A to B through the cavity S₂. The line integral of the electric field (which is nothing but the electrostatic potential except for a negative sign) is positive since the electric field and the line element of integration (a vector) are along the same direction, i.e.: $\Big[\int_A^B \vec{E}\cdot d\vec{l}\,\Big] >0$ .

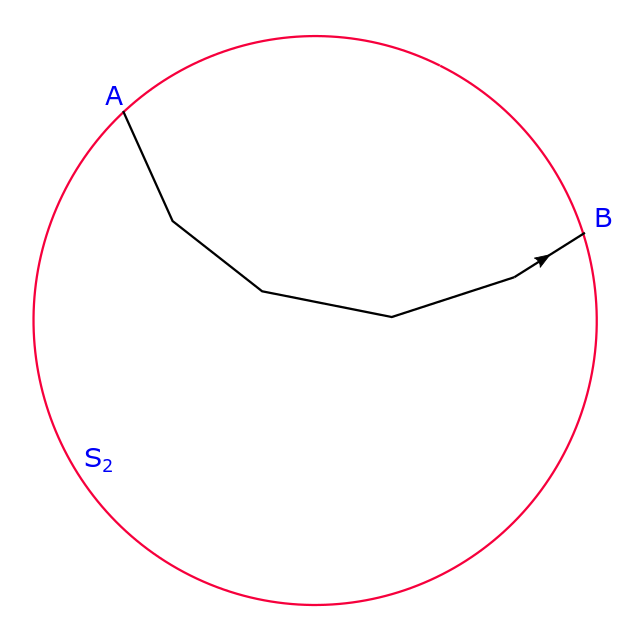
A cavity inside of a conductor. If the cavity has charges on it surface electrostatic field lines must pass through the cavity from one point A on the surface to another point B.

But this integral is nothing but the potential difference (except for the sign as we pointed out above) which must be zero between points A and B as the cavity surface S₂ is an equipotential surface, i.e.: $\Big[\int_A^B \vec{E}\cdot d\vec{l}\,\Big] = \Phi(A) - \Phi(B)=0$ . This contradicts with the first result. But if free charges will be inside of the cavity (or on the surface of the cavity) the net field has to be zero, so charges on surface S₁ and cavity surface (or inside) S₂ will rearrange.

Charge +q resides inside of cavity S2 then induced charges appear on surfaces of S1 and S2 so as to make the field zero again. — Charge +q resides inside of cavity S₂ then induced charges appear on surfaces of S₁ and S₂ so as to make the field zero again.

On the surface of a conductor carrying charges which reside on its surface, higher curvature points will have larger surface charge densities.
Surface layers of charges are assumed to be geometrical planes but due to irregularity of the atomic levels this is not strictly true.

Conductors in Electrostatic Field, Lecture 13.