Tag: optics
-
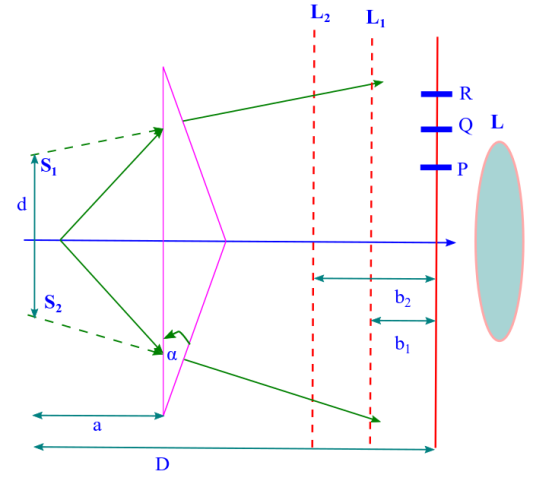
Fresnel’s Bi-prism; measurement of wavelength of light
Optics Series Lecture, Lecture – XI “Fresnel’s Bi-prism: measurement of wavelength of light by it.” Today we will discuss another interesting interference set-up, now that we have discussed the Young’s double slit experiment, in lecture – IX. A few words about the general mechanism behind interference. There are two kinds of interference basically that we…
-
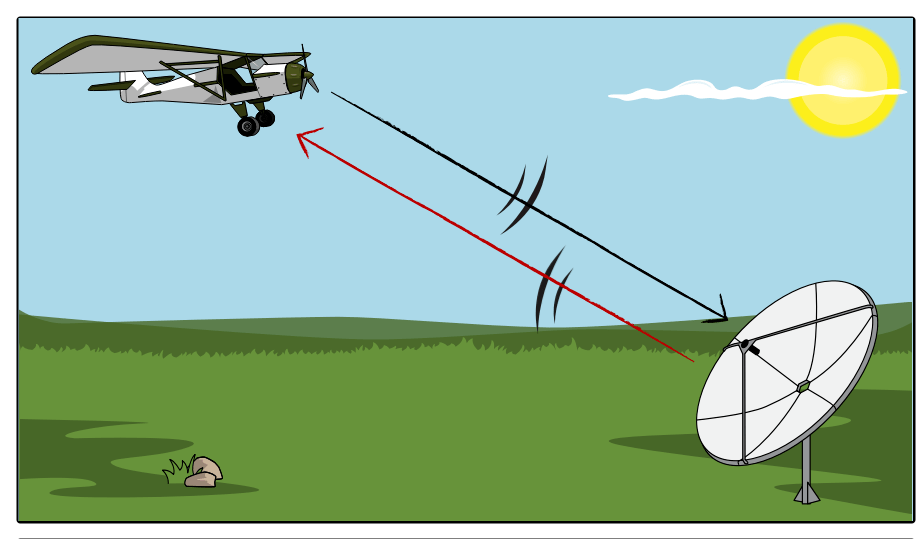
Electromagnetic Nature of Light — A brief history of light.
Let us begin this lecture which has roughly two parts; 1. the history of light and its understanding through the centuries and 2. the electromagnetic nature of light A brief history of light Various optical devices and optical phenomena have been known since close to 4000 years. The optical devices of ancient time includes mirrors, burning…
-
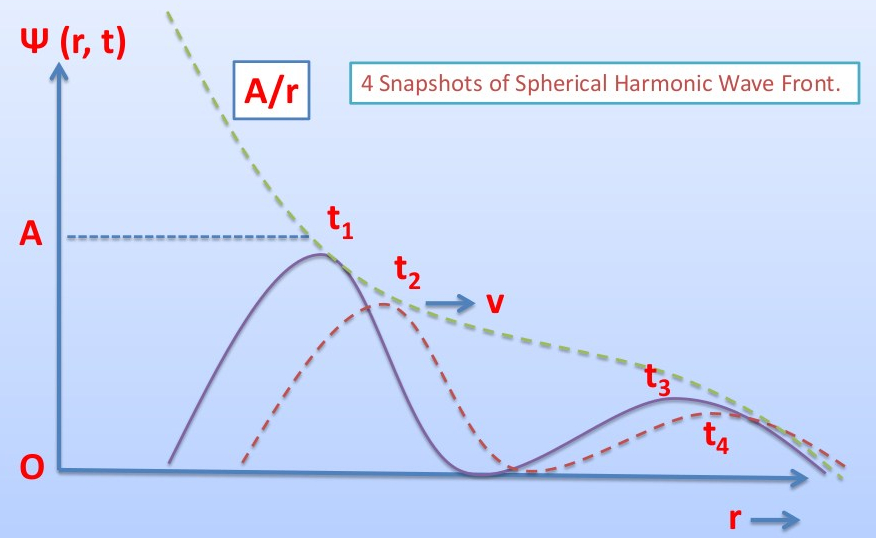
Spherical harmonic waves
In our lecture — VIII, we worked out the form of plane harmonic traveling waves. Note that soon we will have to a. address the concept of wave profile and b. how to convert a wave profile into its corresponding time-dependent or traveling form. But before we do that here is yet another general form of…
-
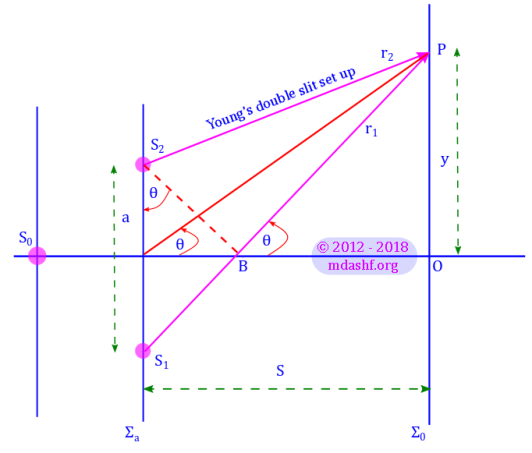
Young’s double slit experiment
Optics Series Lecture, Lecture – IX. “Young’s Double Slit Experiment. Coherent Sources and Conditions of Interference” This lecture was delivered on 14th February in a lecture session of 1 and 1/2 hours. This lecture was delivered to Physics elective students. At a later date this was delivered as a lecture to honors students as well. The…
-
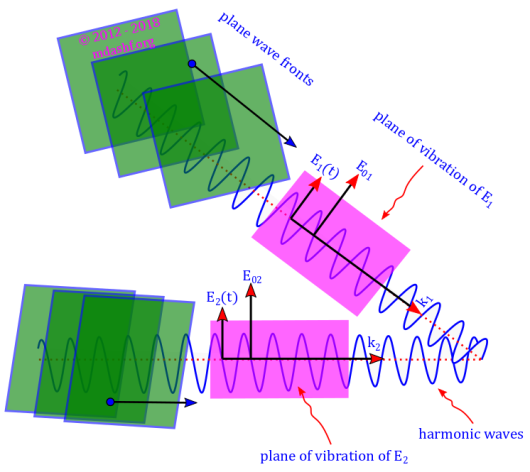
Interference of two plane harmonic waves
Optics Series Lecture, Lecture – VII. “Conditions of interference, Interference of two plane harmonic waves.” This lecture was delivered on 7th February in a lecture session of 1 and 1/2 hours. This lecture was delivered to Physics elective students but intended as a lecture towards Honors students at a later date. Electromagnetic Waves. Light is…