Heisenberg’s energy-time uncertainty as a distance-time and speed-time uncertainty ..
Manmohan Dash
Space rotates around a black-hole. Black-holes like all gravitational objects steal space around them but not all of it. Which means when a photon falls towards a black-hole it is trapped in the space stolen by the black-hole. But since space is rotating the photon might lap onto some space free from the black-hole’s influence. Depending on how the photon is deflected in a game of space and no-space it might come out of this trap.
This is called Hawking radiation — or you can call it Hawking escape. So there is only a very small probability of the photon escaping the photon-sphere of a Black-hole. A photon sphere is somewhat larger sphere than the event horizon. Event horizon is a surface from where material does not escape the trap of Black-hole.
For photons everything is special. The uncertainty which favors escape of photon is Uncertainty principle of Quantum Mechanics. This principle means the actual rate/speed at which space is stolen and appears has an uncertainty. Whether a photon or a material particle such as neutrino or proton the uncertainty relation between energy and time is always an uncertainty relation between speed and time, therefore, actually distance and time.
This means as I described in my article — motion blur, the distance fuzziness is registered even when the time is very sharply known or “selected” by the camera mechanism. This is what you see when you move a little object — in the camera’s image field, while taking its picture, it appears as smeared out or fuzzy.
I have worked out the relation between speed and time uncertainty for an energy and time uncertainty to a very high degree of accuracy, — which is used for our OPERA anomaly paper and is applicable to a wide variety of application in relativistic quantum mechanics.
I will “equationize” for no uncertainty on rest-mass, I can post it here:
Since . — Uncertainty relation of energy-time.
where the large number is a binomial coefficient.
The correct equation is in the order of or Compton wavelength itself as mentioned in our paper. Actually we cite Weinberg’s text for an interesting coincidence between our derived results and Weinberg’s. But Weinberg’s equation is a basic equation of relativistic quantum mechanics which is also described in Landau’s text. I will make an interesting remark on this later.
correct form known from 1930s.
correct form for speed-time uncertainty derived in our paper, consistent with basic quantum mechanics, e.g. Landau QFT or relativistic quantum mechanics.
Energy-time uncertainty is a distance-time, speed-time uncertainty even a rest_mass-time and momentum-time uncertainty as we have given in detail in this referred paper. Actually this is perhaps derived for the first time ever.
If there is any uncertainty on rest-mass, that is, if it is not a nominal mass but derives from other relativistic equations — such as kinematic combinatorics in particle reactions, then there will be additional terms here.
This is a very fundamental equation I worked out so its applicable to a wide variety of studies. When I use this for OPERA neutrinos, I obtain a minimum error or uncertainty on speed of neutrino to be 5.217 mm/s. This is an oversight error, which has been fixed to 2.09 m/s for the basic minimum worked out in the referred paper.
Note that this is remarkable since general relativistic fallout on speed due to earth’s gravity is also a few mm/s order, such as flyby anomaly which I have solved — to very approximate order and summarizing a paper on it. This remark remains correct even though I have fixed the oversight from mm/s to m/s scale, the reasons are explained in detail in this paper.
OPERA sees 7.5 km/s fallout which goes above photon-speed. This will be consistent with relativity theory if the experiment incurred a larger error on their energy while at the same time keeping their time uncertainty between 1 to 10 nano-secs.
So they need to show us their energy distribution with uncertainties, for either event-by-event — 20 neutrinos will be fine, or all-of-it together of the neutrinos — they have 15000 neutrinos. If they give me just one energy uncertainty “I will tell them” they can or can not claim superluminal neutrino.
Their both papers are silent on any energy uncertainty in their measurement. Its a very easy thing to check. One needs to plot the invariant mass distributions of the neutrinos and take the minimum energy resolution eg the smallest bin size is the least uncertainty they make in energy or mass with consistent unit and dimension, this was ~17000 KeV in MINOS 2007 results and so on as described in our paper.
One has to be consistent because we have constrained a 10 KeV to be superluminal whereas a 71 KeV to be consistent with speed of light and larger uncertainties to be non-superluminal neutrinos. Also in this referred paper we have cited other state of the science measurements in similar experiments and energy scales.
Note that the above equation I gave for Δv can be used, except, this is true only when they use a sharp value for neutrino mass. If they use eg kinematic methods in their analysis to use this value then one more exactly similar equation will go into this equation. These details can be easily worked out into our analysis in the paper referred.
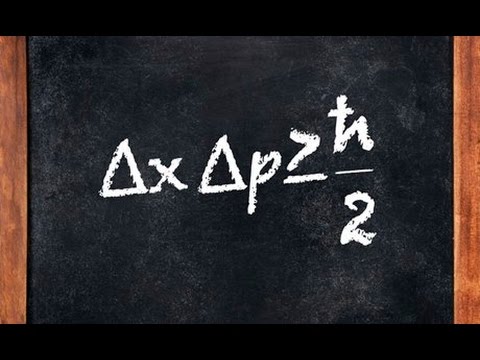
Leave a comment