Lectures on Quantum Mechanics — new series of lectures – QL-3.
All articles in this series will be found here. Click on link to left or just search for menu “Quantum Lectures” on top.
Quantum Lecture Series: Compton effect, Quantum Lecture 3.
This article belongs to a group of lectures I intend to prepare for their online dissemination — without prior preparation to be delivered in a physical format, such as a hand written note to be delivered in a classroom full of students. This series is on quantum mechanics and bears the name sake Quantum Lectures and the number of the lecture will be appended to the end to reflect the same. eg this particular lecture will be named QL-3.
In the meanwhile if you can’t wait and you need some quantum concepts at the earliest, here are two slide-share presentations I had made roughly 5 years ago that consists of most of “some of the things” an undergrad needs along with some solved problems from Griffith’s introductory text on quantum mechanics: quantum slides 1, quantum slides 2. There are other slides on different topics at that account of mine on slideshare.net (such as electromagnetic waves, and these are quite well received by the community for their usefulness).
Compton effect
A new “wave has particle nature” effect
As we have mentioned earlier, we would be discussing a few experiments that elucidates the nature of the new theory based on the ideas of quantization and wave-particle duality. This lecture will be an addition to the phenomenon of photoelectric effect that we discussed in our last lecture, as an example of how a classical mechanics wave behaves in terms of a quantum mechanical particle.
classical vs quantum mechanical particle
We call it a quantum mechanical particle because it has additional properties that are beyond what can be considered a classical mechanics properties. eg the photon always has a definite energy (classical mechanics particles can have a wide range of value for the same) the photon has zero mass, only waves in classical mechanics aren’t associated with mass, particles always have mass. Similarly the energy and momentum are what a wave has, in classical mechanics, without having any mass, but in case of a quantum mechanical particle (such as electron) momentum of wave can also come because its associated with a particle of mass.
This follows from the contrasting properties of a classical mechanics particle (electron) giving credence to a quantum mechanical wave (a wave associated with a mass), but all in all the particle (electron) is no more a classical mechanics particle but a quantum mechanical one, as its properties are starkly different from the former. There are many more interesting properties but I am afraid we will lead ourselves astray if we follow that route.
Principle of complimentarity
A word of caution though when we say quantum mechanics is based on the completely new idea of material objects being wave and particle both, it does not mean they exhibit the same at the same instant of time. In-fact when we discussed our lecture one, we mentioned that wave and particles are distinct entities in classical physics. So quantum mechanics merely entails they are no more completely distinct entity. The same object (lets say a photon, or an electron) can now at times exhibit wave behavior and at other times particle behavior, that these dual behavior are merely complimentary to each other is embodied in the principle of complimentarirty. For a particular set of properties specified, wave behavior can essentially exclude particle behavior and vice versa.
Compton’s experiment and a new effect.
X-ray scattering and Thomson’s scattering theory
In 1923 A. H. Compton, performed an experiment in which he allowed x-ray to be scattered through a block of material (graphite). This elucidated the particulate nature of the classically understood electromagnetic waves. X-rays were discovered 28 years ago, in 1895 and were understood to be high frequency electromagnetic waves. According to the then theory of X-ray scattering developed by J.J. Thomson, the electric field component of the electromagnetic radiation is oscillating and in turn acts on the electrons in the atoms of the material being probed. The atom’s electrons in turn oscillate with the same frequency as that of the electric field of the incident wave.
Thomson scattering
It was known from classical theory of electromagnetic waves that accelerating charges produce electric fields and magnetic fields. In the special case that these fields obey the transverse nature of an electromagnetic wave and fields are tied to each other with specific properties of such a wave, it constitutes a propagating electromagnetic wave with the same frequency. Thus scattering simply means change of direction of the incident electromagnetic wave without any change in its frequency. This is therefore named as Thomson scattering.
X-ray diffraction
X-ray scattering was initially being studied by C.G. Barkla using interpretations from J.J. Thomson’s theory that we mentioned above. In general his experimental results matched well with the theory of Thomson. But there were some anomalies especially for hard X-rays (which are high energetic x-rays, soft in physics would mean low energetic, as hard would mean high energetic). In his time measurement of X-ray wavelength (or equivalently frequency or energy) couldn’t be performed precisely. But soon enough Bragg and M. von Laue established that precise determination of wavelength of X-ray is possible with X-ray diffraction in crystals. This made possible the Compton’s experiment.
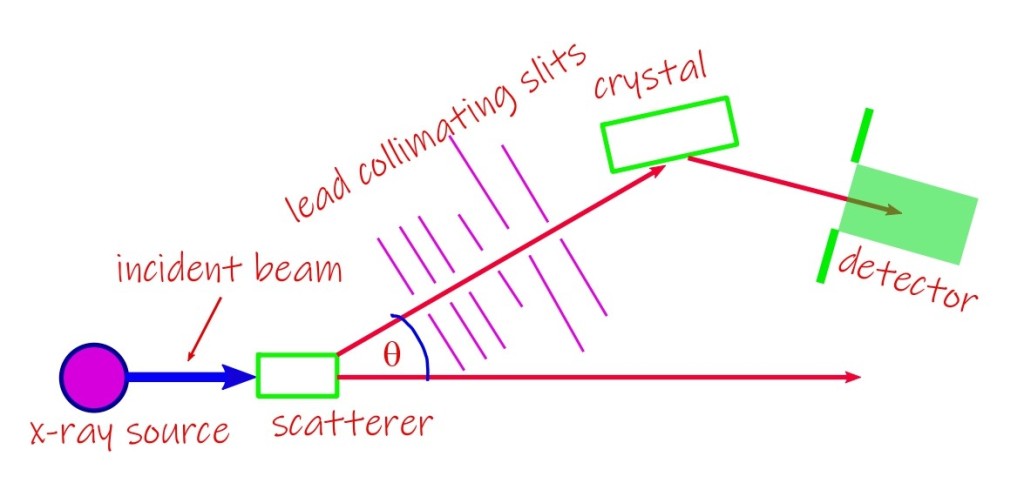
Compton’s experiment set-up
The experimental set up employed by Compton is shown in the following diagram.

Compton irradiated a graphite target with X-rays. He used a monochromatic beam of the same at wavelength λ0. He measured the intensity of the scattered radiation as a function of wavelength. His results are shown in the plot in the following diagram.

He observed that the scattered intensity peaked at the original wavelength if he peeks at the same angle as that of the incidence. But at other angles, as shows the above plot, there appeared another peak at a wavelength λ1 that is higher than the wavelength of the incident radiation, i.e. λ1 > λ0. This was known by the name Compton effect and the classical model of Thomson that we mentioned above was incapable of explaining this occurrence.
The shift of wavelength between the two peaks: Δλ = λ1 – λ0 known as Compton shift depended upon the angle of scattering and was found to be proportional to sin2 (θ/2). Here θ is the angle between direction of the incident beam and the scattered beam. It was found that Δλ was independent of λ0 and the material used and the proportionality constant is 0.048 × 10-10 m.
Compton suggested that the modified line at the secondary wavelength is produced because of the loosely bound electrons in the atoms of the target. These are considered free as their binding energy is small compared to the energy of the incident X-ray beam.
This is why the shift is independent of the material used.
We now consider the scattering of the X-ray photon by a free electron, where the latter is considered to be essentially at rest. The speed of the electron (after it recoils in the collision with the photon) changes to relativistic values, and we must use relativistic kinematics. The energy of a relativistic particle of rest mass m that moves with speed v is given by: E = mγc2 where γ = (1 – v2/c2)-1/2 the Lorentz factor. Kinetic energy is the excess of energy E over rest-mass energy mc2, so K = E – mc2. Momentum of the particle is now: p = mγv. Note that the block letters here signify 3-vector quantities.
If we square the energy and the momentum we see that they satisfy: E2 = m2c4 + p2c2. This is a general equation valid for both mass-less particles as well as particles with relativistic mass. This equation is known as Einstein mass-energy-momentum relation. (The short form energy-momentum relation, could be misleading) Note that we derived it from equations that are valid for particles with relativistic mass such as electrons. i.e. the definitions we gave for energy and momentum above are valid only for such particles and not mass-less particles like photons. Those particles which have a relativistic mass (like electrons) always have a non-zero rest mass (divide the relativistic mass by the Lorentz factor γ). Some people take that to mean those particles which have no relativistic mass must have a zero rest mass.
Bam, thats there they threw the physics into its demise. (They didn’t work out simple math cited above, nor did they think a tiny bit over the physics here) Rest mass is simply not definable for photons. And something that can’t be defined can’t be said to be equal to zero (it can’t be defined because photons are perpetually moving at speed c and hence no rest frame can be defined). To see this mathematically try to find factor γ for photons. Its 1/0 (indeterminate isn’t it?) Then it can’t be divided by zero (photons relativistic mass) to give you zero (the claim that this is now rest-mass of photon). As a result relativistic mass can both be zero (photons) and non zero (eg electrons). But rest-mass is always non-zero (electrons and neutrons eg). When its not its undefinable. (photons)
The way out is to realize that the definitions we gave for electron’s energy and momentum aren’t valid for photons but the relation that electrons satisfy (the mass-energy-momentum relation) is a more general relation (which represents the conservation of energy principle) and photons satisfy this principle as well, from where by placing m = 0 for photon we see that photon’s momentum and energy satisfy a special relation: E = pc. Anyway photon’s energy comes from E = hν = hc/λ (its a classical mechanics wave, it has no mass but still momentum and energy) So before becoming a quantum particle photon had in its origin a classical wave and this is causing all this confusion. Photon is just a special particle and we must remember the above facts. (Many prestigious text books have committed this mistake) This website has a few articles in the past half-decade or more that has tried to brought out this discrepancy in Physicist-speech.
So coming back to the business of the hour, we have photons whose momentum is now: p = E/c = h/λ. The diagram below shows the collision between the rest-less photon and the electron waking from its slumber, kicked by the photon.

Lets now describe the situation depicted in the diagram above with our newly gained mathematical apparatus. The incident photon has an energy: E0 = hc/λ0 and magnitude of momentum: p0 = E0/c = h/λ0. This photon collides with the electron (rest mass m) at rest. After the collision the photon is scattered with energy E1 = hc/λ1 and magnitude of momentum p1 = E1/c = h/λ1 in a direction that makes an angle of θ with the initial direction (direction of incidence). The electron recoils with a magnitude of momentum p2 making an angle of φ with the incident direction.
Now lets apply the principle of conservation of momenta: p0 = p1 + p2. In terms of scalar components this reads as: p0 = p1 cos θ + p2 cos φ and 0 = p1 sin θ – p2 sin φ. Its easy to do some basic algebra and trigonometry and this leads to p22 = p02 + p12 – 2p0p1cos θ. Lets now apply the principle of conservation of energy: E0 + mc2 = E1 + (m2c4 + p22c2)1/2. If we denote the kinetic energy of the electron after the collision by K2 its given by: K2 = (m2c4 + p22c2)1/2 – mc2 = E0 – E1 = c(p0 – p1). From here its easy to see that (rearrange the previous expression and square) p22 = (p0 – p1)2 + 2mc(p0 – p1). This when we combine with the earlier expression for p22, (p22 = p02 + p12 – 2p0p1cos θ) we obtain: mc(p0 – p1) = p0p1(1 – cos θ) = 2p0p1 sin2 θ/2.
Lets now multiply both sides of the above expression (leftmost and rightmost side) by h/(mcp0p1) (recognizing that λ0 = h/p0 and λ1 = h/p1). This leads us to: Δλ = λ1 – λ0 = 2λC sin2 θ/2. This expression for the shift in wavelength is known as Compton Equation. Here λC = h/mc is known as the Compton Wavelength for the particle with mass m (here m is the electron rest mass, hence Compton wavelength for the electron). The calculated value for 2λC matches well with the experimentally obtained value of 0.048 Angstrom.
The unmodified component in the scattered radiation (corresponding to wavelength λ0 of the incident x-ray) results from the scattering by tightly bound electrons, in which case the entire atom recoils from the horror of the incident X-ray photon, when the atomic mass M is used instead of electron mass m, the resulting wavelength shift Δλ is negligible. This also means there is no Compton shift to be observed for light from visible region, as energy of visible range photons are not large even compared to binding energy of loosely bound electrons. As another contrasting situation the shift observed from very high energetic γ-rays only the secondary peak (λ1) is observed as their energy is much large compared to even the binding energy of tightly bound electrons.
Leave a comment