Lectures on Quantum Mechanics — new series of lectures – QL-2.
All articles in this series will be found here. Click on link to left or just search for menu “Quantum Lectures” on top.
Quantum Lecture Series.
This article belongs to a group of lectures I intend to prepare for their online dissemination — no hand written notes of the same is available as I did not deliver these lectures, its an attempt at on-the-fly preparation of the concepts, exclusively available at this website. This series is on quantum mechanics and bears the name sake Quantum Lectures and the number of the lecture will be appended to the end to reflect the same. eg this particular lecture will be named QL-2.
This series will be slower and all-encompassing — as far as my motives are concerned. But if you can’t wait you need some quantum concepts at the earliest here are two slide-share presentations I had made roughly 5 years ago that consists of most of “some of the things” an undergrad needs along with some solved problems from Griffith’s introductory text on quantum mechanics: quantum slides 1, quantum slides 2. There are other slides on different topics at that account of mine on slideshare.net (such as electromagnetic waves, and these are quite well received by the community for their usefulness).
Photoelectric effect: the particle properties of wave.
Hertz’s discovery of photoelectric effect
In 1886-89, (at the age 29-31, and deceased barely at the age 36) Heinrich Rudolf Hertz, a German physicist, performed experiments in which he conclusively established the existence of electromagnetic waves, proposed by the theoretical works of James Clerk Maxwell, a Scottish scientist who unfortunately did not live to see this. Maxwell lived only for 48 years. This was based on the wave theory of classical electromagnetism. But it also led to the description of light in terms of its particulate nature: photons.
Hertz observed that when light in the form of ultraviolet radiation is incident on certain metallic electrodes sparks are produced. Lenard and others showed the production of electric charges from these metallic surfaces. Such a process is named photoelectric effect, — the electric effect of photons sounds like a good brief expansion. Lenard was able to measure the charge to mass of these particles and identified them to be electrons.
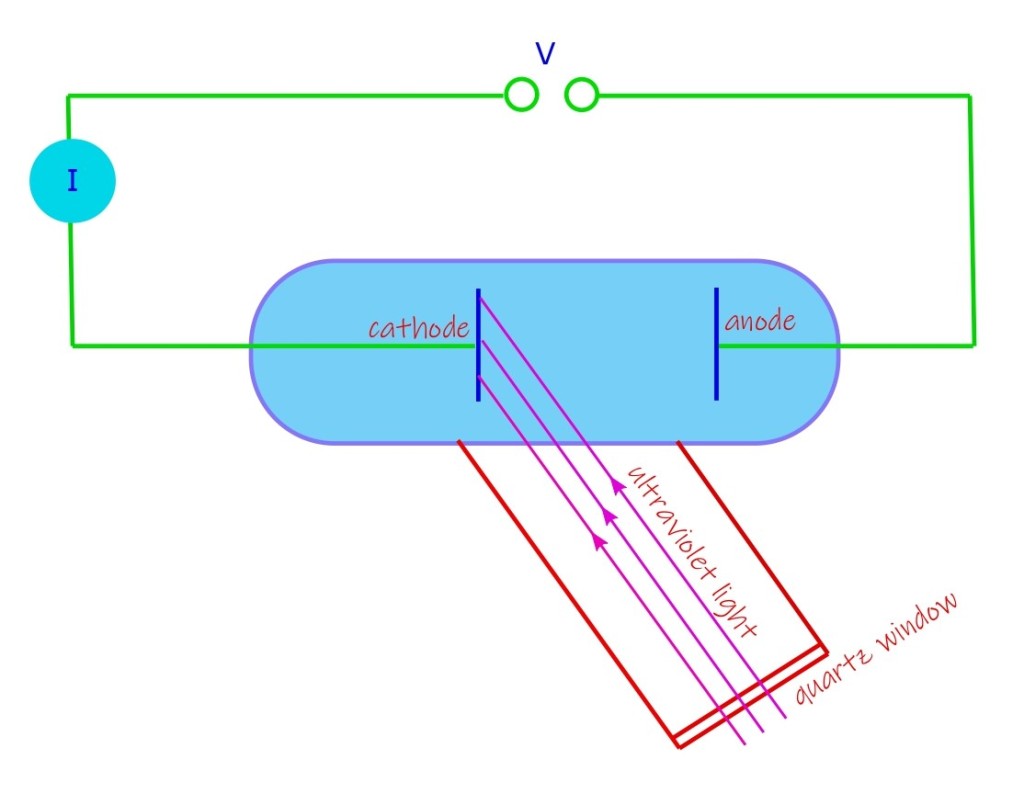
Lenard’s photoelectric experiment, set up
Lenard’s photoelectric effect set up is shown below in its simplified schematic.

Its an evacuated glass tube where ultraviolet light is allowed to be incident on a metal plate (named as cathode in diagram) which is polished. This is known as a photo-cathode and it emits electrons when light falls on it. When some of these electrons have sufficient energy to reach the anode they constitute an electric current I in the external connected circuit. Lenard aimed at studying the behavior of this current when a potential is applied between the electrodes (cathode and anode, as labelled).
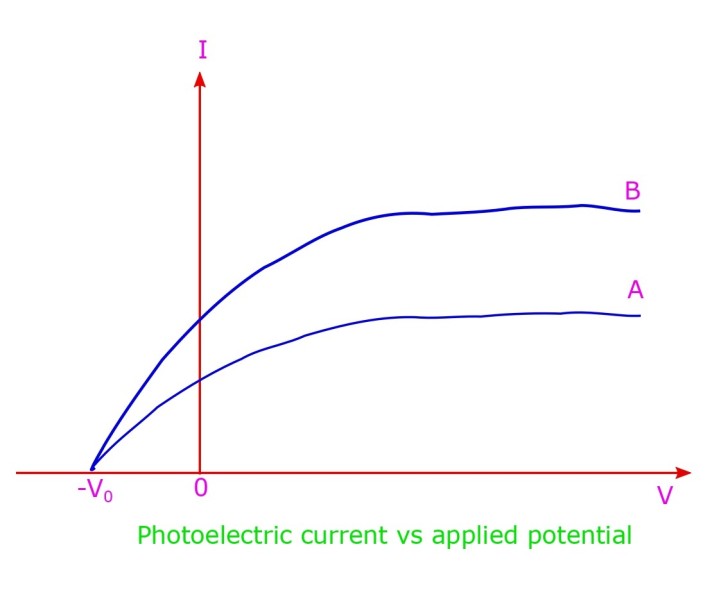
Lenard’s observation on photoelectric effect
The variation of I vs V is shown in the above diagram. For positive potential V, the electrons are seen to be rushing towards the anode (electrons being negative they are attracted towards the anode which is set at positive potential, in this case). With increase in V the current I is seen to increase and eventually saturates, for a large value of V, when there are no more electrons to be emitted.
When a reverse potential is applied, the cathode is more positive wrt the anode and photoelectric current eventually stops, the motion of electrons being impeded by the adverse sign of the applied potential. At potential -V0 the photo-current entirely ceases, this signifies the voltage which is sufficient to stop the emission of the electron from the cathode metallic surface, completely. Thus it was understood that photo-electrons are emitted with a maximum velocity vmax corresponding to maximum kinetic energy (1/2)m(vmax)2 which is equal to the potential energy corresponding to the applied reverse potential. i.e. eV0 = (1/2)m(vmax)2. This potential V0 (in reverse) is therefore aptly called as “stopping potential“. There is a distribution of kinetic energy for the electrons with some having maximum because those which are emancipated from the surface have the maximum kinetic energy but those originating from inside have to pay energy levies at toll gates while commuting to the surface.
The photoelectric current I was found to be proportional to the intensity of the incident ultraviolet light. According to the classical wave theory of electromagnetism number of electrons emitted per unit time should be proportional to the intensity of the light (the light is a wave according to the classical theory). Hence current I being proportional to the intensity is in accordance with this understanding. But there were a few daunting paradoxes posed by the experimental findings that caused serious consternation with the classical theory.
failure of classical physics to explain photoelectric effect
- The surface of emission is associated with a critical or threshold value of frequency of incident radiation (νt) below which no emission takes place. This is independent of the intensity of incident light or the duration for which light is allowed to be incident. But in the understanding of the classical theory any frequency of incident radiation should be able to cause photoelectric effect as long as the intensity of radiation is large enough to impart sufficient energy to the photo-electrons.
- The stopping potential V0 and the maximum kinetic energy Tmax of the photo-electrons were found to be linearly dependent on the frequency and independent of intensity of incident light. But classical theory suggests that the maximum kinetic energy of the photo-electrons should increase with increase in the intensity independent of the frequency.
- There is no detectable time-delay between when light is incident and when the electrons are emitted. According to classical theory since energy of a wave is spread across wave fronts it needs time to accrue sufficient energy to impart to the atom to dislodge the electrons.
Einstein’s explanation of photoelectric effect: the application of the idea of the quantum
Einstein generalized the idea of the quantum postulated by Max Planck and prepared an explanation for these paradoxes of the photoelectric effect in 1905. Remember its one of those famous 5 papers Einstein had published that year — known as Annus Mirabilis or year of miracle, and its this work for which Einstein was awarded the Nobel prize for the year 1921. Planck had proposed that energy of absorption and emission in black body radiation is not available in a continuous manner but in terms of quanta of energy of finite value. We have discussed this in our last lecture.
Einstein generalized this to suggest this quantization is inherent in the wave itself, in terms of particles that carry this quantum of energy, named photons. A photon then has an energy of E = hν = hc/λ. The photons being particles now one whole quantum of energy can be absorbed by a single atom in the metallic surface. When an atom receives this energy an electron can be ejected from the surface.
But not all electrons reside in the surface or escape from there and additional energy is needed to be supplied to actually produce photo-electrons. This minimum additional energy W is characteristic of the metal and is known as work function. Thus maximum kinetic energy, frequency of incident light and work function are related in the following manner: (1/2)m(vmax)2 = hν – W. This is known as the Einstein’s (photoelectric) equation. The threshold frequency (νt) can now be determined from the work function since at this frequency vmax = 0. and so: hνt = W.
Number of electrons emerging from the metal surface per unit time is now proportional to the number of photons striking the metal surface in unit time. Also the intensity of incident light is proportional to the number of photons incident on a specific area per unit time, as such photons carry a definite energy of: hν. Thus the photoelectric current is proportional to the intensity of incident light and all the paradoxes have been taken care of nicely by Einstein’s new theory of photoelectric effect. (Lets revisit to some time around 1905 to see the jubilation on Einstein’s face when his theory was corroborated).
Millikan’s photoelectric experiment
Millikan performed a series of experiment between 1914-16 to confirm Einstein’s theory. From eV0 = (1/2)m(vmax)2 and (1/2)m(vmax)2 = hν – W the stopping potential V0 satisfies a straight-line relationship with the frequency ν: V0 = (h/e)ν – (W/e). Millikan plotted his experimentally obtained values of V0 and ν, and indeed obtained a straight line, from its slope (h/e) and his earlier value for e from his oil drop experiment he obtained the value of Planck’s constant which was quite respectable in the contemporaneous times. He could use visible light and Lithium, Sodium, Potassium surfaces which have small work function properties.
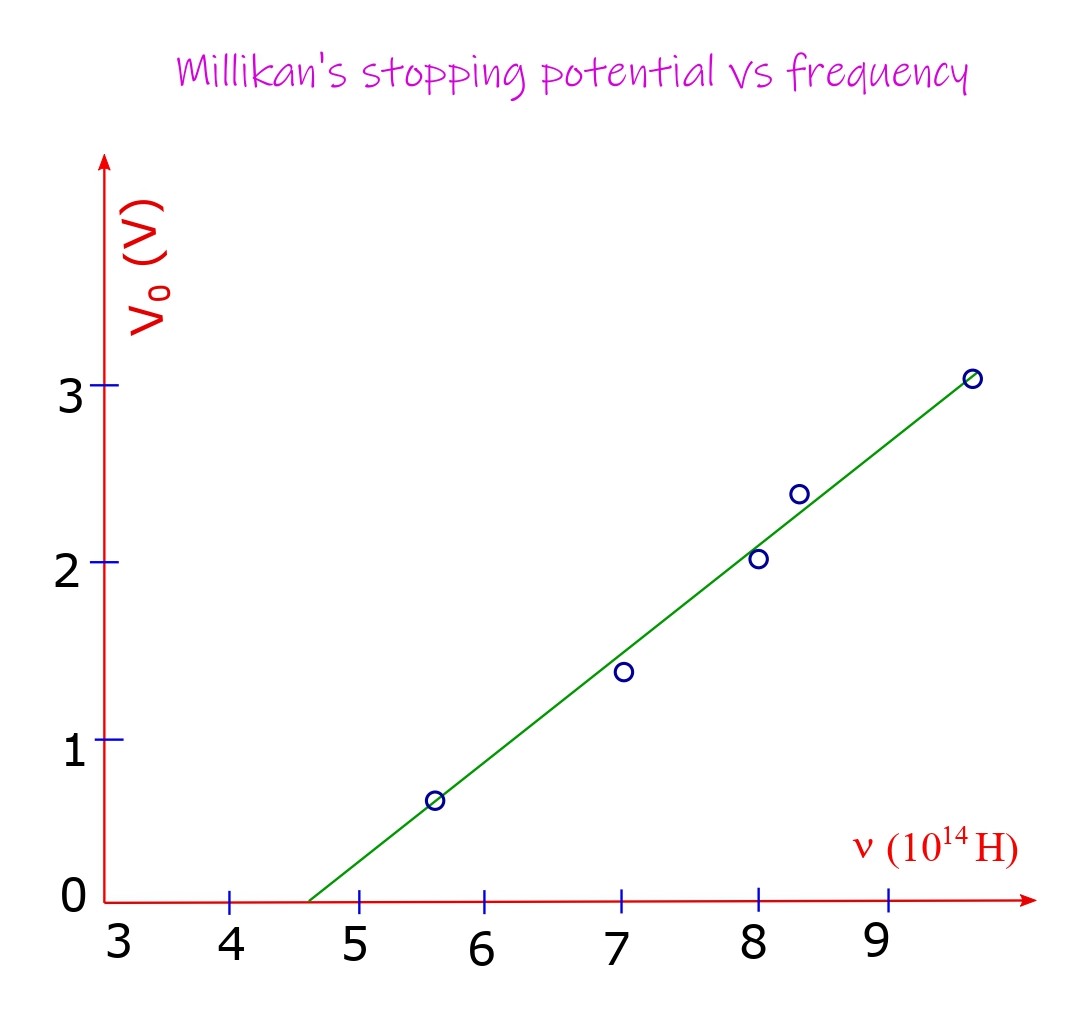
Photoelectric effect is an evidence for the particle nature of light. Nonetheless diffraction and interference provide the contrasting wave nature of light. This duality of light is incompatible with the classical theory but is an inalienable aspect of the new theory called quantum mechanics.
Leave a comment