Black body radiation, Quantum Lecture 1.

Lectures on Quantum Mechanics — new series of lectures – QL-1.

All articles in this series will be found here. Click on link to left or just search for menu “Quantum Lectures” on top.

Quantum Lecture Series.

This article belongs to a group of lectures I intend to prepare for their online dissemination — no hand written notes of the same is available as I did not deliver these lectures, its an attempt at on-the-fly preparation of the concepts, exclusively available at this website. This series is on quantum mechanics and bears the name sake Quantum Lectures and the number of the lecture will be appended to the end to reflect the same. eg this particular lecture will be named QL-1.

This series will be slower and all-encompassing — as far as my motives are concerned. But if you can’t wait you need some quantum concepts at the earliest here are two slide-share presentations I had made roughly 5 years ago that consists of most of “some of the things” an undergrad needs along with some solved problems from Griffith’s introductory text on quantum mechanics. quantum slides 1, quantum slides 2. There are other slides on different topics at that account of mine on slideshare.net (such as electromagnetic waves, and these are quite well received by the community for their usefulness).

Classical Physics Vs non-classical physics: the origin.

Classical Physics till 20th century

By the turn of the last century (1900) the priorities of physicists dealt with several significant reconsideration. By that time classical physics was the cornerstone of all that the physicists wanted to solve about our physical universe. It had its clear signature by the time Galileo was solving physical problems and it had refused to die down for well over 3 centuries, of-course it had received numerous refinements and additions over all these years, — consider eg calculus or differential equations being used to solve the trajectories of planetary motion.

Classical physics had in its fold two massive and competitive facets of the physical nature of objects and phenomena surrounding us. One facet was about using Newton’s laws of motion for predicting the kinematics and dynamics of physical matter. The other facet was about wave motion and its unique phenomena (such as diffraction or interference, for saying it out loud). The latter had culminated in an all explaining framework of Maxwell’s electromagnetic equations. These two facets were clearly distinctive in their formulation and appeal.

Theory of Relativity

At the turn of the century came the theory of Relativity propounded by one of the most iconic faces of scientists: Mr Einstein, the eccentric genius. This did change the priorities of physicists in many unwelcoming and forceful ways: the most beautiful theories are the ones that are substantiated by the all illuminating facts of experiments, and the insightful theories of Einstein were one of the luckiest in that respect. These theories critically examined and removed some of the most honorably held aspects of classical physics, nonetheless these theories are included into its fold, as the latest understanding. Fundamentally there wasn’t anything startlingly different in these theories from the nature of classical mechanics. You can call the two theories of relativity as new classical mechanics and the former the old classical mechanics — but they are still; Classical mechanics.

Classical mechanics (the old or former) is easily reproducible from the new theories of relativity by realizing them as the manifestation of relativistic principles at very small velocities, compared to the speed limit of universe, the speed of light in vacuum. Theories of relativity (the special and the general versions of it) did not wipe out the distinction between matter and radiation (wave) as two separable entities.

A new theory: origin of the quantum

In the last quarter of the penultimate century and the first of the succeeding, to that, i.e. roughly 1875 to 1925, there were a slew of experimental findings that broke this lovey-dovey relationship between physicists and old or classical physics. These findings gradually brought in new or modern explanations and concepts into their fold that the physicists eventually had to concede to. (Remember Einstein’s “God does not play dice” but He might still enjoy watching it right?) This is the reason the new theory that developed in the time frame — roughly 1900 to 1930, is known as Modern Physics (as opposed to old physics) and Quantum Mechanics as opposed to classical physics. Its therefore based on the idea of a quantum and in this lecture we will begin our sojourn into the world of quantum. We will study about some of those experiments.

The new theory introduced some of the most profound ideas on which its based. They are:

• quantization of physical quantities such as energy or angular momenta,
• particle properties of radiation (or wave, we can use them interchangeably) and
• wave properties of particles.

Planck’s constant and the quantum of action

All these new ideas are intertwined with a new universal physical constant so small that your mother in law might have a hard time believing it. But hey its real, its called Planck’s constant denoted by the letter h. Why h? I know not. Well some people think it represents the word: Hilfsgrösse, which means its not a primary variable, probably just there to aid the other big-shots. But that apprehension turned out to be a false bravado. But its smallness in size (and not in spirit) is what brings theory of relativity closer to quantum mechanics. This is why some people think theory of relativity is not classical physics. But those who formulate the naming in physics are something like the elite King and kinship of Saudi Arabia. Their political power is absolute and exclusive. Make peace with it. Relativity is related to quantum mechanics in one way other facets of classical physics are not. Small is fast. Small for quantum mechanics and fast for relativity. This is why you would often see h and c hangin together in bars and ** clubs (and of-course in physics equations). On a serious note Planck’s constant is known as the fundamental quantum of action.

Black-body Radiation

It was known that the surface of a hot body emits energy in the form of electromagnetic radiation. It is a process that occurs at any temperature other than the absolute zero, the energy being distributed over a continuous range of all wavelengths. But when temperature is not very high, say less than 500 ⁰C, the relatively longer wavelengths are what the energy is radiated at most prominently. Long wavelengths correspond to the infrared radiation.

An increase in temperature causes this prominence of energy of radiation to shift to the shorter wavelengths. The radiation corresponds to visible light within 500 ⁰C to 600 ⁰C and the body appears white hot at 3000 ⁰C — incidentally this is the temperature of the radiation that filled the Universe when it was 1 million years old, it has cooled down to -270 ⁰C over the 12.8 billion years. The total emitted power increases as well with temperature in addition to its redistribution over the wavelengths.

When radiation is incident on bodies some of it are reflected and rest is absorbed. Actually as we will see shortly some is also transmitted, but what matters is whats absorbed and whats not. Dark colored bodies absorb most of the incident radiation, while most of it is reflected by light colored bodies. One can define a quantity called “absorptance” as the “fraction of the incident energy thats absorbed by a body“. “fraction of the incident energy thats absorbed by a body at a given wavelength” would then be the “spectral absorptance“. When a body is at a constant temperature which signifies thermal equilibrium, equal amount of energy per unit time is absorbed as well as emitted. This is so otherwise the temperature would inflate or plummet depending on which is more, absorption or emission. Radiations absorbed or emitted at thermal equilibrium are referred to as thermal radiation.

A note here is imminent about the types of processes that we just mentioned. There are 4 things that are happening as regards to the process of thermal or any kind of radiation. A. Reflection (goes off the surface) B. Transmission (goes through the body but isn’t attenuated or altered) C. Absorption (soaked in by the body) and D. Emission (released by the body). Do not confuse between emission and reflection, its easy to do that.

A black body is one which absorbs all and reflects (or transmits) none of the incident radiation. Consequently its absorptance is 1, at any wavelength. Black body radiation is the name of the thermal radiation absorbed or emitted by a black body. Before understanding the idea of the black body in more detail here are a few definitions that are in order, in order that we grasp the idea of the black body better.

The definitions of a few important fundamental quantities

• Total energy density: the total energy density at any point is the total energy of radiation, per unit volume considered at all possible values of wavelengths. Its denoted by the symbol u.
• Spectral energy density: this is the energy density per unit wavelength at a given wavelength. i.e. its the energy per unit volume per unit wavelength at a given wavelength. Its denoted by the symbol u_λ. u_λdλ denotes the energy per unit volume in the wavelength range λ to λ+dλ. It is related to the total energy density by the integral relation: .
• Total emissive power or emittance: The total emissive power of a body is defined as total energy emitted (integrated over all wavelengths) per second per unit surface area of the body. Its denoted as e.
• Spectral emissive power or spectral emittance: Its defined for a particular wavelength λ. Its the energy emitted per unit range of wavelength per unit surface area in a second. Its denoted by the symbol: e_λ. Thus e_λdλ denotes the energy emitted per unit area per second at that wavelength. Its related to total emissive power through the integral expression: .
• Absorptance: fraction of the incident energy thats absorbed by a body, per unit surface area per second. (its integrated over all wavelengths). Its denoted by the symbol a.
• Spectral absorptance: fraction of the incident energy thats absorbed by a body, per unit surface area per second, at a given wavelength. Its denoted by the symbol a_λ. If δQ_λ denotes the energy incident per unit area per second at that wavelength, from all possible directions then a_λδQ_λ is the amount thats absorbed per unit area per second at that wavelength. Its related to total absorptance through the integral expression: .

The above parameters (u, e, a, u_λ, e_λ, a_λ) depend on the temperature at which the body is found and e, a, e_λ, a_λ depend on the nature of its surface as well (except for a black body). Note that a perfect black-body is defined from the parameters a, and a_λ. These 2 parameters (of absorption) are dimensionless whose maximum value can be unity.

A note of caution

Note that a widely followed textbook on thermal physics that I have been following a lot gave the correct definition of total emissive power but named it as emissivity, thats like giving correct definition for resistance and calling it resistivity. Its otherwise a good textbook. Also a widely followed textbook on quantum mechanics that has in recent years become my most preferred one too, called absorptance (spectral absorptance) as absorption coefficient, which actually is one whole lot different than he intended it to refer to. This is also a really good book otherwise.

One should really be cautious of such tripping over.

Ideal and perfect black body.

If we define r_λ as the fraction thats reflected, t_λ as the fraction thats transmitted and a_λ as the fraction thats absorbed then together: r_λ + t_λ + a_λ = 1. A perfect black body is one that has a_λ = 1, as r_λ = 0 and t_λ = 0.

There are no perfect black bodies in nature but the following can be a very good idealization of the same. Consider a cavity as shown in the figure above, which is kept at a constant temperature. Its interior walls are colored black. An outsider sees the hole as a black body surface. Thats because any radiation thats incident on the hole, is almost absorbed by the walls of the cavity after multiple reflections inside it. This means the absorptance of the hole is equal to unity. The cavity being in thermal equilibrium any radiation inside of it and any radiation escaping through it can be considered black body radiation. The hole behaves as a black body only at a lower temperature though where the wavelengths of emitted radiation are longer than that of visible light.

Kirchhoff’s law

From purely thermodynamic arguments Kirchhoff proved (way back in 1859, much before the quantum debate were to take place) that “ratio of spectral emissive power (i.e. e_λ or spectral emittance) to the spectral absorptance (a_λ) is the same for all bodies at a given temperature — that is its a universal function which depends only upon wavelength of radiation and the equilibrium temperature of the body in consideration, and is equal to the spectral emissive power of a black body (E_λ) at that temperature“. i.e. e_λ/a_λ = E_λ.

Note that the right and left hand side of the above equation (Kirchhoff Law’s mathematical form) are universal functions of λ and T. i.e. as long as we hold λ and T captive and do not tinker around them, i.e. as long as we simply alter the bodies of consideration (alter their nature i.e.) but not these two variables, the ratio in the left hand side should be a constant.

This means if emissivity (ratio of emissive power e_λ to emissive power of a black body E_λ, at a given temperature) is higher so is absorptivity a_λ.(absorptance is already a fraction “absorbed”/”incident” and absorptance of a black body is one, so absorptivity is equivalent to saying absorptance, in our case spectral absorptance).

An efficient absorber is also an efficient emitter. A black body is the most efficient absorber as well as emitter.

There is a very very easy to prove the Kirchhoff’s law. The way Kirchhoff proved it and another rigorous way to prove the same is given in Thermal Physics by Garg, Bansal, Ghosh from Mc Graw Hill publication. Here is the easy way.

Let δQ be the thermal energy incident on an unit surface area per second on a body of consideration (between wavelength λ and λ+dλ, we have suppressed λ for brevity). The quantity of radiation the surface will absorb is then a_λδQ. a_λ here is its spectral absorptance (or absorptivity, we can use this interchangeably only for a_λ as we have discussed above).

As we have seen above remaining energy must either be reflected or transmitted, but in general both. Since e_λ is the spectral emissive power e_λdλ is the amount of energy emitted per second from an unit surface area (in the wavelength window of λ and λ+dλ). Total energy thats given out is then: (1 – a_λ)δQ + e_λdλ. For the body to be at equilibrium, this must equal to the amount of energy incident on it. i.e. δQ = (1 – a_λ)δQ + e_λdλ.

This simplifies to a_λδQ = e_λdλ. For a perfect black body absorptivity a_λ is 1 and e_λ = E_λ. Thus δQ = E_λdλ.Using this result in the expression (a_λδQ = e_λdλ) we get: e_λ/a_λ = E_λ which is the form of the Kirchhoff’s law we began with.

Stefan-Boltzmann law

Sometimes for the black body the total emissive power (E) is denoted as R. They probably stem from the words (E)mission and (R)adiation respectively. But we will continue with E. In 1879, Stefan found an empirical relation between total emissive power and the temperature of a body: E(T) = σ T⁴. Here σ is the Stefan’s constant given as: σ = 5.67 × 10^-8W/ (m²K⁴). See how easy it is to remember this: 5,6,7,8, one just needs to remember where the fraction and power goes and the units. Boltzmann was able to derive the same from thermodynamics arguments and thus its known as Stefan-Boltzmann law. Lets now consider the black body radiation. We have seen above: , i.e. the total emissive power is the integral of the spectral emissive power over all wavelengths. So for the black body: , by the Stefan-Boltzmann law. Since E the total emissive power of the black body is a function of temperature only it follows that the spectral emissive power of the black body E(λ,T) is as well a universal function, this is in line with the expectations of the Kirchhoff’s law that we had discussed above.

Wien’s displacement law

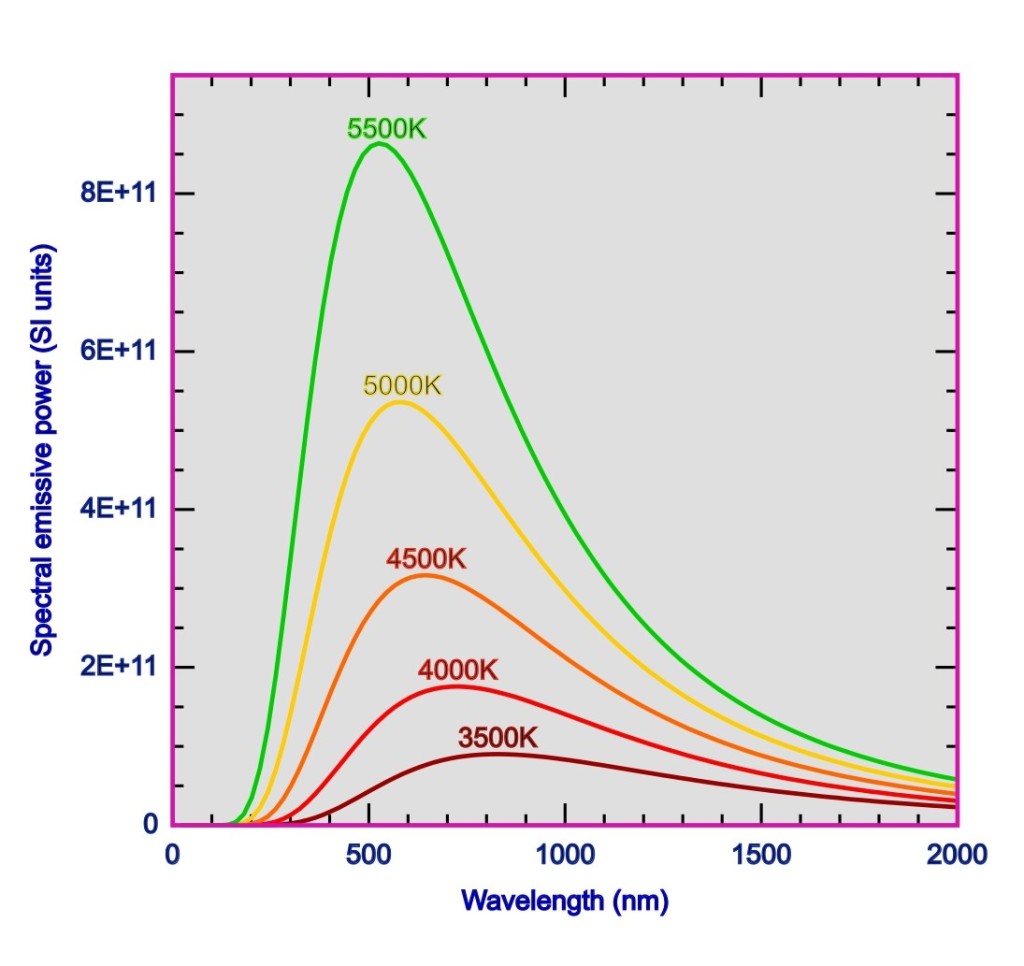
The first accurate measurements of this universal function E(λ,T) the spectral emissive power or spectral emittance of a black body were performed by Lummer and Pringsheim, in 1899, and the spectral emittance vs wavelength are shown for various temperature in the following diagram.

What we see above in this plot is given a particular value for the wavelength the emissive power is more if the temperature of the emitting body is more. What we also see is there is a particular value of the wavelength at which the curve has a peak, i.e. at this wavelength (denoted by: λ_max) there is maximum emittance from the body. And this peak shifts leftwards i.e. towards shorter wavelength when temperature increases. Thus there is a linear relationship between this wavelength associated with maximum emittance and temperature: λ_maxT = b. This is known as the Wien’s displacement law. This constant b is known as Wien displacement constant with a value b = 2.898 × 10^-3 mK.

In the idealized notion of a black body being represented by a cavity with a small hole, as depicted by a diagram above, whose walls are uniformly heated to an equilibrium temperature, the hole emits black body radiation, the inside of the cavity is also filled with the same. Based on second law of thermodynamics Kirchhoff proved that this radiation is isotropic (same in all directions) as well as homogeneous (same at all points) and identical in all cavities at the same temperature, and all this being valid for any given wavelength.

Wien’s law

Instead of spectral emissive power E(λ,T) it is easier to use an alternate variable known as spectral distribution function or monochromatic energy density: ρ(λ,T). Its the energy density i.e. energy content per unit volume specified at a given temperature and a specific wavelength. Its related to the spectral emissive power by a constant factor: ρ(λ,T) = 4/c E(λ,T). From general thermodynamic arguments Wien in 1893 showed that this distribution function has the following functional form: ρ(λ,T) = λ^-5f(λT), f(λT) can’t be determined from thermodynamics. Its easy to show that Wien’s displacement law and Stefan-Boltzmann law are contained in this equation which we can call Wien’s law. But the constants b and σ can’t be determined until form of the function f(λT) is known.

Rayleigh-Jeans law

The idea

Rayleigh and Jeans made an attempt at deriving this function f(λT) and ρ(λ,T) from laws of classical physics. They considered the radiation inside of the cavity as consisting of standing electromagnetic waves. They determined the number of such waves, i.e. number of modes of oscillation of the electromagnetic field in the cavity per unit volume when these waves were within the wavelength window of: λ and λ+dλ, this number per unit volume per unit wavelength turned out to be: 8π/λ⁴. The spectral distribution function is then the product of this number with the average energy (ε) in the mode with wavelength λ. i.e. ρ(λ,T) = ε × 8π/λ⁴.

atoms as oscillators

They argued that the atoms in the walls of the cavity act as electric dipoles i.e. linear harmonic oscillators with frequency: ν = c / λ. These oscillators create the radiation in the cavity by constant absorption and emission at such frequencies. The energy ε can take any value between 0 and ∞. At thermal equilibrium the average energy of these oscillators (ε) can be obtained by weighting ε with Boltzmann probability distribution factor (e^-ε/kT) using the laws of classical statistical mechanics. Here k is the Boltzmann constant and we can write: β = 1/kT.

finding the average energy of an oscillator

From the definition of average we have: . Recognize that the Boltzmann factor is simply a frequency factor (its proportional to the probability of occurrence) and the denominator therefore gives total number of occurrences. The denominator is called the “sum of states“, Zustandssumme or partition function. (this is usually denoted as Z in stat-mechanics, Z from Zustandssumme) The numerator is a given value multiplied by the frequency of its occurrence (i.e. probability) summed over all the values. Hence the ratio is an average (Basic definition of average is: ∑w_ix_i / ∑w_i). So our weight (e^-ε/kT) corresponds to w_i.

equipartition energy

From basic calculus the average can be written as the derivative of the log of the denominator — this is a quite frequently employed trick in statistical mechanics, so get along with it, any time you see, it will greet you with a smile. We have now: . This is nothing but the classical or statistical mechanics law of equipartition of energy — that average energy at equilibrium is equally shared per a degree of freedom, with a value of kT/2. Adding this value once for kinetic energy of the oscillator and once for potential energy, we get the average value kT.

The spectral distribution function or monochromatic energy density

Thus the spectral distribution function according to the ideas of Rayleigh and Jeans turns out to be: ρ(λ,T) = (8π/λ⁴)kT. This is the famous Rayleigh-Jeans distribution law of thermal physics. We now see that the function f(λT) that was sought after with utmost yearning is found according to Rayleigh-Jeans to be: f(λT) = 8πk(λT).

Ultraviolet catastrophe

A plot between the spectral distribution of energy with wavelength from experiment and a comparison with the Rayleigh-Jeans distribution law is shown in the following diagram.

In the long wavelength region Rayleigh-Jeans law matches with the experimental values, but when we go to the short wavelength region (λ→0), it shoots up to the sky. There is no expected maximum and it diverges. This means the total energy density becomes infinite: . This can not be a physical case therefore and is referred to as ultraviolet catastrophe.

Planck’s Quantum Theory

There was nothing in classical physics that could help evade the problems that were unleashed by ultraviolet catastrophe. But Max Plank presented a new form of distribution of oscillator energy (and therefore radiation emissive power) by piggy-riding on a revolutionary idea: that of a quantum. While the community wasn’t in easy heartbeats to accept such an uncanny idea, it nevertheless dealt a heavy blow to the catastrophe and solved the problem. And it turned out to be a correct idea, despite of its lack of foolproof logic, in the beginning.

Max Planck postulated that energy of an oscillator at a given frequency ν can’t take arbitrary values between 0 and ∞. Rather they can only take discrete values of nε₀. n is a positive integer or zero. ε₀ is a finite amount or quantum of energy and it may depend on frequency ν. Then assuming the Boltzmann factor to be valid for this problem, the average energy of an assemblage of oscillators of frequency which are all at thermal equilibrium is given by: .

By substituting the expression for average energy as before, Planck obtained his energy density distribution law: . In order for this to satisfy Wien’s law ε₀ must be proportional to the frequency. So ε₀ = hν = hc/λ. Here h is a fundamental physical constant as we have discussed in the beginning of the lecture, and called Planck’s constant. Its called the fundamental quantum of action as its got the dimension of [energy-time], [length-momentum] and action. Its very small in size. Whenever a physical quantity of a system with the dimension of action expressed in units of h is very large then the quantum effects are negligible. If its comparable to h on the other hand, quantum effects must take precedence.

The Planck’s famous spectral distribution law now becomes: . Its easy to show that at longer wavelengths this is in agreement with Rayleigh Jeans law and goes to zero at shorter wavelengths. At long wavelengths the quantum of energy is small compared to the thermal energy kT and the quantum states are distributed continuously: this validates classical equipartition law. But at short wavelengths quantum states are widely separated (quantum of energy is large) they can be accessed only by absorption of highly energetic quanta. They are unavailable for lower values of quanta. Therefore these processes are rare and as a consequence the equipartition law isn’t valid anymore, the spectral density can safely go to zero, at the shortest wavelength evading the fatal consequences of ultraviolet catastrophe.

The value of λ for which energy density is maximum can be obtained by differentiation of the Planck’s expression given above, as a result λ_max T = hc/(4.965 k) = b. The total energy density is now finite (the triumph of Planck’s idea of quantization) and: ρ_tot = aT⁴, with a = (8π⁵/15)(k⁴/h³c³). Since ρ_tot = 4E/c and E is taken from Stefan-Boltzmann law, this gives us Stefan’s constant σ = (2π⁵/15)(k⁴/h³c²). These equations relate b and σ to 3 fundamental constants c, k and h.

The success of Planck’s idea of the quantum

Planck’s idea of a quantum of energy not only successfully solved the problem of the black body radiation but also numerous others. It successfully explained the existence of a cosmic background radiation remnant of the big-bang explosion from when it was 1 million years old and the radiation existed at 3000 ⁰C to now when its at 3 K i.e. -270⁰C. We briefly mentioned this fact in the introduction to this lecture.

Einstein took the idea of quantization of energy of Planck one notch up and said its not only the energy which is quantized but the physical entities such as the electromagnetic field itself. The quantization of the latter gives rise to photons the quantum particles of light, which are then in equilibrium with the quantum oscillators, the atomic dipoles. Thus photons have specific quantized energy dependent on their frequency or wavelength and a fixed speed. This he successfully extended to explain the process of photoelectric effect which we will study in our next lecture and to explain the specific heat of solids. Debye further improved on Einstein’s quantum ideas and made a fitting match with experimental evidence for the specific heat. We will know more about specific heat theories of Einstein and Debye in our Solid State Physics lectures, which have already begun to be cast in their online version (but the hand notes that I developed and delivered my lectures on, are not with me right now, due to lock-down from COVID-19).

Apart from this Planck’s idea had its indelible impression on Compton effect (we will study this anon), existence of atomic line spectra and Stern-Gerlach experiment and the wave properties of matter, eventually opening the vast vista of Quantum Mechanics as we know today. Planck’s quantum idea was a fertile seed after all.