Electromagnetic theory, lecture — I
This lecture the first lecture in the electromagnetic theory series for the physics honors class, was delivered on 21st December 2017.
All electromagnetic theory lectures of this series, will be found here.
“Maxwell’s equations in free space and in material media”
Also read part-2 of the linked lecture. That describes the subject matter of this lecture, in a good deal of depth.
Topics covered
A. Maxwell’s equations — basic form
B. Displacement current — Correction to Ampere’s law
C. Maxwell’s equations — in material media
Maxwell’s equations
Maxwell’s equations the basic forms
The Maxwell’s equations without the corrections to the Ampere’s law can be written as the following;
(i)
(ii)
(iii)
(iv)
where is the electric charge density and
is the electric current density.
The equation (i) which says that the divergence of the electric field vector is proportional to the electric charge density, is known as Gauss law — of electrostatics.
Electrostatics is when the electric charge and electric current densities ( ,
), that produce these field, known therefore also as the sources of the field, do not explicitly depend on time, that is, are constants.
These sources or distributions depict the behavior of the field, and their independence from time means the fields do not vary in time, but vary only under spatial transformation.
Note that we are not talking about sources in the Maxwell’s equations above, but the ones that actually produce the and
fields of the equations.
The sources present in the Maxwell equations above would alter these static fields though. Accordingly the Maxwell equations would change their behavior in dynamic — i.e. time varying conditions, than they exhibit in the static conditions.
Equation (ii) has no names, but sometimes given a name, Gauss law — of magneto-statics.
Equation (iii) is known as Faraday’s law — of electromagnetic induction.
Equation (iv) is known as Ampere’s law.
Inconsistency in Maxwell’s equation
The Maxwell’s equations in this form are not the most general form of the eponymous set of equations. Also they are fraught with some degree of inconsistency.
Lets gaze deeper.
Lets state a basic mathematical result: Divergence of curl of a vector is zero, identically for all vectors.
Let us apply “divergence” to equation (iii).
We see that L.H.S. is zero from the vector identity we stated above.
But from the equation (ii) of Maxwell equations — which says divergence of the magnetic induction vector is zero, .
So we see that both Maxwell equation (iii) and the vector identity can be satisfied simultaneously.
Let us check this up on equation (iv). Let us apply the same process to equation (iv).
The L.H.S. is zero from the vector identity. But the R.H.S is not zero in general as is quite arbitrary. The current density
can be non-zero — irrespective of whether its steady — for static magnetic field, or non-steady — for dynamic magnetic field.
Another way to look at this problem is to look at the integral form of Ampere’s law — equation (iv).
Maxwell’s correction of Ampere’s law and displacement current
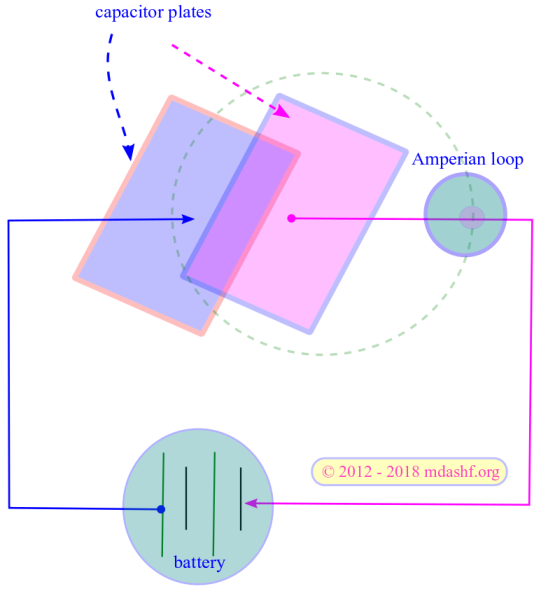
Let us try to understand this through the circuit configuration shown in the figure below.

If we consider a plane surface as shown — in gray, whose circular boundary is the Amperian loop, enclosed current is given by, current passing through the circuit. But if instead an inflated surface is drawn whose bounded area gives the same Amperian loop then no current passes through this surface,
.
Lets apply equation of continuity: and Gauss law:
.
By substituting this extra factor , the inconsistency in the Ampere’s law was fixed by Maxwell.
Thus
The resulting equation is known as Ampere-Maxwell equation or the modified Ampere’s law.
is known as the displacement current.
This signifies that a changing electric field produces a magnetic field just as a changing magnetic field produces an electric field. These are no more electro or magneto static processes but electro-or-magneto-dynamic processes. This generalizes the Maxwell’s equations as well as remove the inconsistencies.
The resulting general equations are known as Maxwell’s equations as we would quote them today. These are given as:
(i)
(ii)
(iii)
(iv)
Maxwell’s equations in matter or material media
It is more convenient to cast the Maxwell’s equations into a different form when the fields are considered in various material media. Then we have electric and magnetic polarisations given by vectors, and
.
The electric polarisation vector which stands for the number of electric dipoles in an unit volume is related to the bound charge by the following relation.
Similarly .
Apart from this a change in polarisation is associated with a polarisation current, given by;
.
So, .
Thus the total charge consists of free and bound charges.
But
Then Gauss law becomes: ,
with: .
So, .
Ampere’s law becomes: ,
with: .
So, .
Thus in terms of free current density and free charge density Maxwell’s relations are now:
(i)
(ii)
(iii)
(iv)
and
are related to
and
through constitutive relations, which are given for linear media — also called simple media, below.
where
and
.
Leave a comment