Application of Gauss Law – Cylindrical and Planar Symmetry, Lecture-2

Lectures on Electricity and Magnetism — new series of lectures – EML – 2

All articles in this series will be found here. Click on link to left or search for menu “E AND M BASICS” on top.

Application of Gauss Law To Problems with Cylindrical And Planar Symmetry, EML-2

In our last lecture we laid a good foundation about the concepts of electric field, lines of force, flux and Gauss Law. It can be found here; EML1. Today we will discuss how to apply Gauss Law to find the electric field if cylindrical or planar symmetries are present in the problem.

+ click to see more about this article

This article belongs to a group of lectures I intend to prepare for their online dissemination — these were delivered in a physical format, beginning with hand written notes that were delivered in a classroom full of students. This series is on Electricity and Magnetism and bears the name sake Electricity and Magnetism Lectures and the number of the lecture will be appended to the end to reflect the same. eg the current lecture will be named EML – 2 . This lecture was delivered to honors students on 31st Jan 2017.

In the meanwhile if you can’t wait and you need some of these concepts at the earliest, here is a slide-share presentation I had made roughly 5 years ago that consists of “some of the things” an undergrad needs: Electricity and Magnetism slides. There are other slides on different topics at that account of mine on slideshare.net (such as; Introduction to Quantum Mechanics , and these are quite well received by the community for their usefulness).

Cylindrical Symmetry

Infinitely long rod of uniform charge density

An infinitely long rod of negligible radius has a uniform (linear) charge density of λ. Calculate the electric field at a distance r from the wire.

An infinitely long rod possesses cylindrical symmetry.

Electric field E must be radially outwards from axis of symmetry of the rod, — for +ve charge.

Consider a Gaussian surface which is cylindrical. Magnitude of the field E (|E|) is constant on the surface of the cylinder of radius r. A Gaussian surface is one closed surface that conforms with the symmetry of the situation and encloses a given amount of charge whose electric field is to be determined.

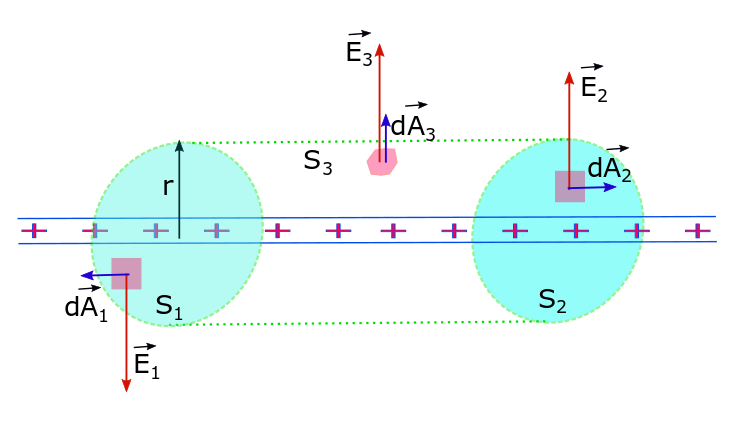
The amount of charge that is enclosed in the Gaussian cylinder is given by: q_encl = λl. Here we have assumed that a linear charge density — i.e. charge per unit length λ is carried by the rod and the Gaussian cylinder has a height/length of l. See the diagram shown below.

There are 3 components of the cylindrical Gaussian surface: side-caps S₁ and S₂ and curved surface S₃. We can accordingly write the flux for each one of them (where the electric field is uniform over the entire surface component) and add them up for the total flux that emerges out of the Gaussian surface.

$\Phi_E=\iint_S \vec{E}\cdot d\vec{A}=\iint_{S_1} \vec{E_1}\cdot d\vec{A}1+\iint{S_2} \vec{E_2}\cdot d\vec{A}2+\iint{S_3} \vec{E_3}\cdot d\vec{A}_3=0+0+E_3 A_3=E(2\pi rl)$

Now we can apply Gauss Law: Φ_E = E(2πrl) = λl/ε₀. This gives us the electric field strength (magnitude) of the infinitely long uniformly charged rod; $\boxed{E(r)=\frac{\lambda l}{2 \pi \epsilon_0}\frac{1}{r}= (2 k \lambda l)\frac{1}{r}}$ .

A Gaussian surface that is cylindrical in shape encloses the similarly symmetrical charge distribution of a portion of an infinitely long rod of +ve charge

We can now plot this field strength as a function of the radial distance. We can also show the cross sectional view of how the field direction looks like. The following two diagrams show these two aspects respectively.

The field strength of an infinitely long uniformly charged rod plotted against the radial distance from axis of symmetry.

The cross sectional view of direction of electric field strength of an infinitely long uniformly charged.

Planar Symmetry

Infinitely large non-conducting plane

For an infinitely large non-conducting plane in the xy plane with uniform surface charge density σ; determine the electric field everywhere in space.

The configuration has planar symmetry.

Electric field E is perpendicularly away from the plane. We can thus write $\vec{E}=E \hat{k}$ . The field is constant on planes parallel to the non-conducting plane.

Uniform surface charge density on an infinitely large non-conducting plane, has planar symmetry.

Lets choose a cylindrical Gaussian surface as shown in the following diagram, its called a Gaussian pillbox.

The infinitely large uniform surface charge distribution on a non-conducting plane is straddled by a Gaussian pillbox, one that serves as the Gaussian Surface.

The total charge enclosed is obviously σA where A=A₁=A₂ is the area of the end-cap.

Total flux is given by: $\Phi_E=\iint_S \vec{E}\cdot d\vec{A}=\iint_{S_1} \vec{E_1}\cdot d\vec{A}1+\iint{S_2} \vec{E_2}\cdot d\vec{A}2+\iint{S_3} \vec{E_3}\cdot d\vec{A}_3=E_1 A_1+E_2 A_2+0=(E_1 + E_2) A$ .

The two ends are at the same distance, so E₁=E₂=E. With that recognition the flux is now given by: Φ_E = 2EA.

Now we can apply Gauss Law as we did earlier: Φ_E = 2EA = q_encl/ε₀=(σA)/ε₀. This gives us the electric field strength (magnitude) of the infinitely large uniformly charged non-conducting plane; $\boxed{E=\frac{\sigma}{2\epsilon_0}}$ . $\boxed{\vec{E}=\frac{\sigma}{2\epsilon_0}\hat{k}, \,\,\, z>0; \,\,\,\\ \vec{E}=-\frac{\sigma}{2\epsilon_0}\hat{k}, \,\,\, z<0}$

The electric field strength of the infinitely large non-conducting plane has two components, along +z and -z.

3 thoughts

Pingback: Application of Gauss Law, Spherical Symmetry, Lecture-3 – M Dash Foundation: C Cube Learning
Pingback: Conservative Nature of the Electrostatic Field and Electrostatic Potential, Lecture – 4. – M Dash Foundation: C Cube Learning
Pingback: Laplace And Poisson Equation, Lecture 5, 6, 7 And 8. – M Dash Foundation: C Cube Learning

M Dash Foundation: C Cube Learning

Invariance: A journal with a difference, where mind meets aspiration

Application of Gauss Law – Cylindrical and Planar Symmetry, Lecture-2