Lectures on Electricity and Magnetism — new series of lectures – EML – 3.
All articles in this series will be found here. Click on link to left or search for menu “E AND M BASICS” on top.
Application of Gauss Law, Spherical Symmetry, Spherical Shell and Non-conducting Solid Sphere Lecture-3
In our last two lectures we laid a good foundation about the concepts of electric field, lines of force, flux and Gauss Law. They can be found here; EML1 and EML2. In the last one we discussed how to apply Gauss Law to find the electric field if cylindrical or planar symmetries are present in the problem. Today we will discuss how to do the same if spherical symmetry is present. In particular we will discuss two cases
- Spherical Shell and
- Non-conducting Solid Sphere
+ click to see more about this article
This article belongs to a group of lectures I intend to prepare for their online dissemination — these were delivered in a physical format, beginning with hand written notes that were delivered in a classroom full of students. This series is on Electricity and Magnetism and bears the name sake Electricity and Magnetism Lectures and the number of the lecture will be appended to the end to reflect the same. eg the current lecture will be named EML – 3 . This lecture was delivered to honors students on 2nd Feb 2017.
In the meanwhile if you can’t wait and you need some of these concepts at the earliest, here is a slide-share presentation I had made roughly 5 years ago that consists of “some of the things” an undergrad needs: Electricity and Magnetism slides. There are other slides on different topics at that account of mine on slideshare.net (such as; Introduction to Quantum Mechanics , and these are quite well received by the community for their usefulness).
Spherical Symmetry in a Spherical Shell
A thin spherical shell of radius a has a charge +Q evenly distributed over its surface. Find the electric field both inside and outside the shell.
The charge distribution is spherically symmetric — i.e. it does not depend upon angular parameters (e.g. in a spherical polar coordinate system) but depends only upon position, i.e. radial distance from center of such a system. We can rotate the sphere (shell) about any radial direction and that won’t change the field value or direction.
The surface charge density is total charge over total surface area over which its found, and this is uniform, i.e. does not change from place to place. So it must be given by: σ = Q/(4πa2).
The electric field magnitude E must be radially symmetric (i.e. uniform for a fixed r, in all directions, as we just discussed above) and its direction must be radially outward (charge is positive and it must exert a repulsive force on a positive test charge which must run away from center, for its life)
Lets represent this pictorially in the following diagram.

The given problem can be discussed in two scenarios, one for the field inside of the shell and the other for the field outside of the shell. Accordingly we discuss case-I and case-II.
Case I: Electric field inside of the spherical shell
The situation in the first scenario, where we would like to determine the electric field strength magnitude and direction at any point inside of the thin spherical shell is depicted in the following diagram. It shows a suitable Gaussian surface which is a concentric sphere inside of the shell whose surface co-terminates at the points where we would like to determine the field value, i.e. r.
Always remember that a Gaussian surface is one imaginary closed surface that conforms with the symmetry of the situation.
The Gaussian surface encloses a given amount of charge whose electric field is to be determined.

For our situation we realize that r ≤ a. The Gaussian surface is a sphere of radius r ≤ a and co-centered (i.e. concentric) with the shell. The charge enclosed is obviously zero, so the net flux is zero as well, from Gauss Law. i.e. qencl = 0, ΦE = (qencl)/ε0 = 0 ⇒ E = 0 for r ≤ a.
Case II: Electric field outside of the spherical shell
The situation in the second scenario, where we would like to determine the electric field strength magnitude and direction at any point outside of the thin spherical shell is depicted in the following diagram. It shows a suitable Gaussian surface which is a concentric sphere outside of the shell whose surface again co-terminates at the points where we would like to determine the field value, i.e. r.

For our situation we realize that r ≥ a. The Gaussian surface is a sphere of radius r ≥ a and co-centered (i.e. concentric) with the shell. The charge enclosed is obviously qencl = Q, so the net flux is given by Gauss Law. i.e. . Thus the electric field strength is given by:
. This expression is same as we would get for all this charge Q to be concentrated at the center.
Below is a plot of the electric field strength as a function of radial position r, for all points, i.e. inside as well as outside of the shell.

Spherical Symmetry in a Non-Conducting Solid Sphere
An electric charge +Q is uniformly distributed throughout a non-conducting solid sphere of radius a. Determine the electric field everywhere inside and outside of the sphere.
The charge distribution is again spherically symmetric. We can write the volumetric charge density (which is uniform, i.e. same at every point inside of the solid sphere) as ρ = Q/V = Q/[(4/3)πa3).
Electric field is radially symmetric and directed outward (for a positive charge). Field strength E is thus constant on spherical surfaces of radius r, in all directions, like we saw before for spherical symmetry. As before we discuss two scenarios.
Case I: Electric field inside of the solid sphere, r ≤ a
The Gaussian surface is a sphere of radius r, so that r ≤ a.

To calculate flux we use Gauss Law: . The charge that is enclosed is proportional to the volume of the Gaussian sphere. So,
.
. Thus the electric field strength is given by:
.
Case II: Electric field outside of the solid sphere, r ≥ a
The Gaussian surface is a sphere of radius r, so that r ≥ a. Its shown in the following diagram.

Here the total charge is enclosed within the Gaussian surface. So obviously qencl = Q. Flux is given by: ΦE = E(4πr2). From Gauss Law: E(4πr2)=Q/ε0. Thus the electric field strength is given by: .
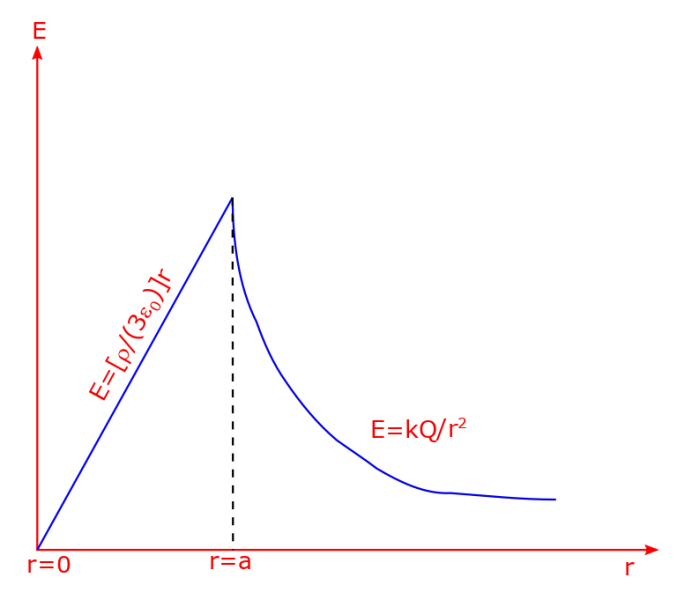
This result is same as the result of having all the charge concentrated at the center. The following plot shows the relationship between the field strength at all points as a function of separation from the center of the solid sphere.

Leave a comment