This article is written in the flow of my intuition which is in a chronological order without any flip-flops. So first I came up with the idea Principle of equivalence means “nature of potential energy and kinetic energy are same” hence they are equivalents, not gravitational mass and kinematic mass, as represented through all texts. [ — read other articles linked in this article for this idea]
Then I came with the idea it actually follows from Principle of Least action, in a round about way [which could be spurious and incorrect but leads to the answer] and in a direct and simple way in two lines.
Introduction
In the linked article “use least variation on integral of action and prove principle of equivalence” written a few days ago, I had proposed a general way to prove the principle of equivalence, from the least action principle. In-fact I had mentioned the equivalence from the equation of motion in a few of the other articles I wrote, about the principle of equivalence and the Newtonian nature of some of most profoundly known Relativity Theory ideas.
I had slightly mentioned this fact: equation of motion leads to the equivalence and also I had mentioned principle of equivalence, should in-fact in its most general form, be stated as Kinetic Energy and Potential Energy are equivalents (not equal).
All these proofs will follow in this article. In-fact prior to all the calculations I did, that I am going to write in this article, because my printers aren’t cooperating with me at the moment so I can simply scan the 11 pages, I had done on pen and paper: I had mentioned these facts of equivalence and other ideas.
Here are all the other articles you may want to read before or after this article:
3 aspects of Relativity of Einstein that are actually Newtonian and
There is a very simple way the equivalence will follow, which I will mention at the complete end. I will go through all the other interesting ideas first.
Principle of equivalence of special Theory of Relativity:
– gravity ≡ acceleration
In the article “I cannot believe this” I have described why principle of equivalence is actually simply: T≡U, then
![]()
or,
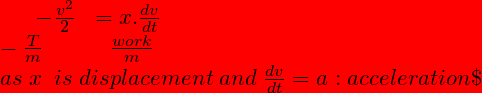
Already it is evident that there is nothing “special relativistic” about Principle of Equivalence ..
This can be called the principle of equivalence in Newtonian Mechanics.
This can also be called principle of equivalence in theory of Relativity as – gravity ≡ acceleration, in general, -T/m =V. {the equality follows from equivalence not from equality in any equation} which says the nature of potential energy is not different from nature of kinetic energy.
Since L=T-U, L=2T only when |T|=|U| in the actual amount of T and V, not equality from equivalence. equivalence is a characteristic and we set the variables equal to infer such properties. In actuality T and V will differ by constants as we will see later.
In other words equivalence applies to the part which is equal, it does not equate two quantities.
In the generality
![]() ,
,
we realize that: x=f(t) and a more general equation may follow from “Principle of least action”, which is
![]()
One also realizes “in the mentioned article”
![]()
is only a condition that must be satisfied in order for principle of equivalence to be valid because K.E. = P.E. will not lead to
![]()
if that were not so. In general one can keep the mass terms and even use the Lorentz Invariant equations and definitions of relativistic K.E.
One scenario is imagined: one could set a relativistic kinematic mass and relativistic gravitational mass slightly different and something like energy conservation may be violated that way ? Just a musing.
The general form of principle of equivalence therefore may be contained in the principle of least action which leads to equation of motion.
Now lets denote x by f(t),
![]() .
.

In principle of equivalence
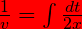
note that, 1/v and dt/x = dt / f(t) are dimensionally consistent. In the 1st two pages I proved the “principle of equivalence” from Newton’s equation of motion x=f(t).
Equation of motion
Equations of motion are a set of differential equation. that gives the “trajectory” of particles in terms of generalized coordinates
![]() .
.
For waves also there exists differential equations called wave equation of motion e.g. acoustic waves, Maxwell equations which are valid for em waves. When an equation of motion deals with both waves and particles its called Schrodinger’s equation:
![]() .
.
A wave-equation is 2nd order in space and time derivative:
![]() .
.
[You can easily check the dimension of the equation by remembering on one side you’ve x, on one side t, so where does v=x/t go? As simple as that.]
The wave-particle equation or Schrödinger’s equation is 2nd order in space {H=p^2/2m}but first order in time. Is it because a particle equation of motion has zeroth, 1st and 2nd order time derivatives? Perhaps. I had asked this question 4-5-6 years ago. Perhaps on a social networking site.
The other feature of Schrödinger’s equation is i and h-cross: quantization and complex number value. Complex number values allow probabilistic nature. Probability when normalized is always less than 1, can be equal if all outcomes are taken into account, is a fraction therefore and e^iθ gives sine, cosine which are bounded by 1 in moduli. Any thing raised to e in this manner is a phase-factor whose complex-conjugate gives 1 when multiplied to the phase factor.
Now we will derive the principle of equivalence
![]()
from principle of least action
![]()
The principle of least action
The principle of least action is also called the principle of stationary action. In my mind stationary perhaps depicts degeneracy or equalness of different paths, i.e. action S is equal and least not just for 1 path but for many. [alternative histories] and they all must be added => quantum mechanics. A least-action is like spending least amount of energy/action/Lagrangian for a “given set of values of a variable” : trajectory.
A trajectory: set of values of a variable.
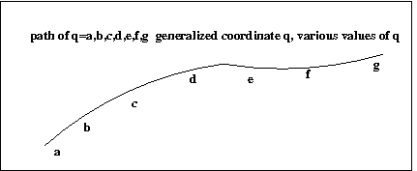
S, L, E for this path is least compared to other paths in the vicinity. Nature is economic in its energy or more appropriately action.

As explained, to buy egg-plants with least “economy” one has to spend $10 for egg-plants available in Blacksburg but $13 for Pulaski.
In other words when there are two variables 1. gas and 2. egg-plants the least is Blacksburg-egg-plants. If only 1 variable of egg-plants were there which is conceptual but not necessarily realistic Pulaski is least.
For nature there may be 1000s of variable and a least action is chosen. The electron takes a path of variables q, q-dot, …. [q=a,b,c .. and q-dot are its 1st time derivatives] such that the least amount of energy/action is spent. q,q-dot, … are called generalized coordinates or phase-space. [In particle physics terminology a phase-space is nothing but the mathematical possibilities of all position and momentum variables which therefore kinematically gives all energy etc, anytime there are kinematic variables position, momentum etc arise you can think/conceptualize all possible values and that would be the phase-space]
Calculus of Variation
action=S=integral{ L dt},
L=Lagrangian=T-U, T=K.E., U=P.E.,
H=Hamiltonian= T+U
T=1/2mvv, U=mV, V=Potential.
![]()
Since U=mV,
![]()
or
![]()
the above depicts Force times displacement is work which is a change in potential energy [which is what we study in sophomore years]
Now Lagrangian is a way of saying “I make a combination of T & U in a more or less “effective” way so that its not easy to “manipulate” “. One could perhaps define action in a more complicated way “from T& U given” and apply a variational calculus to infer something. Just musing.
For a free particle ** []
V=0, L=T-V = mvv/2.
![]()
integrate by parts the above, with e(t)=Lf(t) and dg(t)=dt/f(t);
** [remember free means force-free, hence potential free. Since kinetic energy is equivalent to potential but only when there is acceleration K.E. is changing, hence there is a force, I think, free particle would simply mean K.E. with a uniform velocity. So free means constant velocity or an inertial frame of reference. Why is objects falling under influence of earth or other heavenly bodies called freely falling objects? I think its because the force of gravity is already considered to be external and accounted for. ? Strictly speaking its not a free fall since the motion would be circular if orbiting or accelerated linearly if close to surface. ]
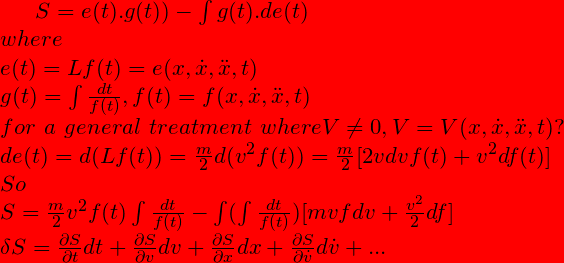
Each partial derivative must vanish if partial of S = action is zero, so
![]() .
.
We have
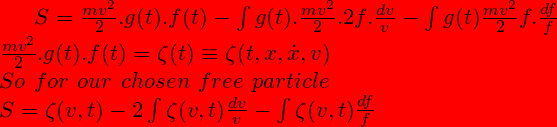
At some point a little while ago we lost the generality of L, we can put the general form back for a general treatment.
for now
![]()
means
![]()
with a= gmvv/2 and db = df we have
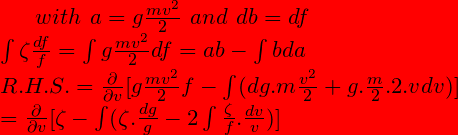
We have a mistake here which I will notify at the end and correct the result. But lets go with this. [some mistakes lead to interesting insights]
So we have,
![]()
You will notice that we have the first terms on both LHS and RHS equal so they must cancel. Now let me tell you the mistake here instead of at the end. The mistake that I committed involves the 2nd and 3rd term on RHS, when we did integration by parts through a and b, db=df so b=f and b=f isn’t multiplied to the 3rd term. By sheer chance, it was multiplied to the 2nd term. Then we should not have a f in the denominator of 3rd term. SO the correct thing is the 3rd term on RHS and 2nd term on LHS are equal and must cancel. That means the 2nd term on RHS is zero. I will easily show that the 2nd term on RHS is indeed zero.
But thats not what I obtained in the first attempt. What I did was I had the f in the denominator and obtained
![]()
Now I show the 2nd term on RHS [for equation above the term on RHS and RRHS] is indeed zero. [which is also zero when we have committed a mistake on the earlier 3rd term on RHS by having an extra f in that term’s denominator]
remember that g=integral {dt/f} by definition hence dg = dt/f with this – del/del-v [integral {zeta.dg/g}] = -del/del-v [ integral {(1/2)mvv.gf.dt/gf}=-del/del-v[t.(mvv/2) – integral{t.mv.dv}] = -mvt + tmv + c(v) = 0 +c(v)
where we have used the fact that derivatives and integrands are anti-integrands and anti-derivatives of each other and the integrand we evaluated is zero arbitrary to a constant of variable of integration, which is v here.
So we have gfmv (1+1/f) = c(v) or g=[2.c(v)/v].1/m(1+f). This is what we set out to prove: g/2=1/v. we have this except for c(v)/m(1+f), f could be free of v(t) for a free particle, i.e. v is uniform or constant ? In that case we have an inertial frame of reference where c(v)/m(1+f) =1 and we have proved principle of equivalence from Least action principle.
Now this is a correct result although obtained with spurious method, there was an unintentional mistake. If we remove that f in the denominator we simply have 0 = 0 by applying calculus of variation to the action integral.
Lets therefore turn our attention to the Principle of least action again, and this is what I promised at the beginning of the article: that I will tell you how simply the principle of equivalence can be obtained from the principle of least/stationary action.
Its just two lines and would have saved a lot of laborious calculation we did in the last few pages. [many pages and iterations on hand may not be on print-copy]. So some mistakes lead to interesting insights, what could be spurious can lead to results that are correct. Whats laborious and full of mistakes need not be rejected from a path of investigation.
Here is the two lines that prove the results for which this whole article was written.
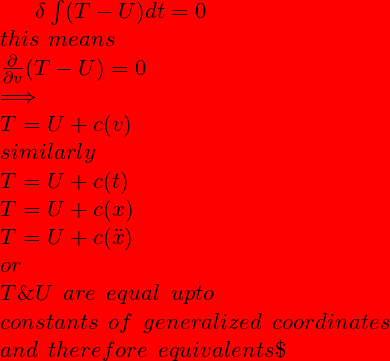
It then evidently and obviously leads to
![]() .
.

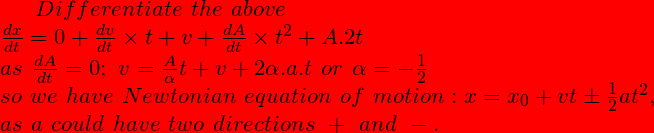
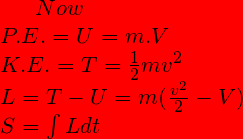
Leave a comment