The angular parameters of celestial mechanics !

If you are one of those geeks, who is always attracted by the technicalities of Celestial Mechanics, I would say, its a good introduction of the study. I have named it “Angular parameters of celestial mechanics”.

These are the understanding you need eg, if you want to do any satellite study, Mars Orbiting or Astro-photography. I was led from the understanding of various kinds of telescopes and mounts to first understand how the coordinate system for our universe are defined, this attempt is midway. But I am done with angular parameters, for the basics, have a glance.

A great circle is a circle that passes on a sphere, so that its radius (or diameter) equals to the radius (or diameter ) of that sphere.

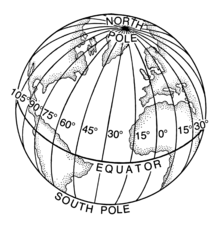
If the great circle goes through one of the poles (– so both poles as an imminent condition of this definition) its also called a meridian and this circles’s angular reference wrt one of all possible meridians is called a longitude angle, or simply longitude.

For a celestial sphere, thus, longitudes or meridians are called an hour angle. To be more discerning one can say the longitudes are the set of great circles, passing through the poles of the sphere. There are by definition 360 of them. Meridian also refers to the circle or its angular position in a well defined reference. That is, it can be used in the sense of a circle or an angular displacement wrt a reference zero.

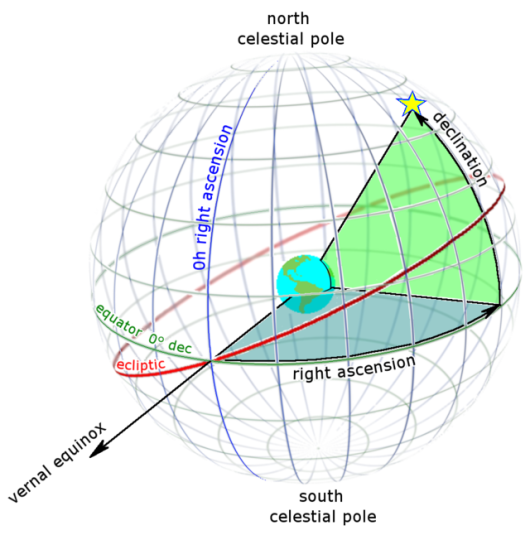
Right Ascension (α) is the angular measurement of the displacement between the vernal equinox and the Meridian of a location or an Hour Circle or a particular Longitude. Or, in other words, between zero hour angle and meridian. So one can say the zero hour angle is the primary direction, which in this case is the vernal equinox (also called First point of Aries).

Note that these angles are measured on the equator plane (the only great circle available on horizontal cross sections of a given sphere) eastwards, from primary direction or zero hour angle.

So its imminent to realize that meridian, hour circle, hour angle, longitude and right ascension are all synonymous with each other. They represent the same geometrical state of mind. (This is important since right ascension is intimate with celestial system and longitude is a geographic equator system, but geometrically they are the same)

Hour Angles are thus the angular reference of the great circles that the Hour Circles are, that pass through one (therefore both) of the celestial poles.

*A pole is one of the two extreme point of a chosen axis of rotation through a sphere.

**A celestial sphere is an arbitrarily large dynamically chosen sphere that can be made to coincide with the geographic sphere of any planetary body eg. eg if you sit in earth (in your room in your arm chair) try looking outward in all possible direction and construct a sphere with its center at center of earth, its equator coinciding with equator of earth and so on.

This large sphere is one example of a celestial sphere. It contains without respect to distance of the most distant objects, such as galaxy and nebula, all such objects which seem to reside on the inner surface of this large celestial sphere.

Equator is thus a (locally) horizontal plane, that crosses through your sphere (earth) and your chosen celestial sphere.

Latitudes (φ) are horizontal circles concentric with this equator (with varying elevation across the actual sphere, named as arctic circle and antarctic circle etc)

Longitudes (λ) are (meridians or hour circles, Right Ascension etc) the vertical circles concentric with vertical great circles of celestial sphere. (circles that pass through poles) …

For celestial sphere meridians or longitudes are called as hour angles, as the great circles (passing through celestial poles ) are called as hour circle.

Also note that instead of circles and spheres we talk about ellipses and ellipsoids in general.

Like the right ascension we also call the latitude angles as Declination (δ), δ is referenced again with primary direction on equatorial plane, along with the North-South running Longitude or Meridian.

Here is a good diagram to show these parameters.

The units are trickier in case of right-ascension but easier in case of declination. For the former, one defines a circle to be 24 hours of angle. Each hour is 60 minute of angle and each minute of angle is again 60 seconds of angle ! Thus the right-ascension angles do not directly correspond to the arc-second or arc-minute units. In-fact, eg, 1 angle minute of RA system is 15 arc-minutes and so on.

(IMP; Sidereal hour angle is -ve in sign with RA hour angle but differs from Astronomical hour angle. Who can expand that into a blog?)

But for declination definition units are like usual arc-minute and arc-seconds, except we need only a quarter of a circle. So we cover a circle in four 90 degrees with each degree giving the regular vantage of 60 arc-minutes and so on.

So basically the RA is a sidereal earth-rotation based unit of angle. Its an angle-cum-time. Call it Timangle?

Note one very important attribute of sphere. The horizontal circles which are called as latitudes (which you define from a particular primary direction as latitude angles φ) provide as many circles as you wish (cutting through various heights of the sphere)

We chose to divide a horizontal circle (latitude circles) into 360 directions; one in each degree of the circle. But only one circle among all the possible concentric circles is a GREAT circle. Its called an Equator, it equates the latitude-circle’s radius to that of the sphere which it cuts.

All other latitude circle that are now non-great circles (that is radii smaller than that of the sphere) can be named. We have thus 5 named circles on latitude. Beginning North we have Arctic Circle on North pole, then Cancer Circle, then Equator Circle, then Capricorn Circle and the bottom most on south pole, Ant-arctic Circle.

But when you draw vertical circles through the sphere all of it are great circles. You are not interested in keeping the non-great circles. Hence as many as you want (we take 360 divisions and call them meridians, the 180-W and 180-E placed at Greenwich) are there and each of them is called a longitude, meridian or hour circle.

There are no special names for one of the circles, because each of them are equivalent around the axis of the rotation of the sphere. Equator is perpendicular to the axis hence one of the horizontal circles is unique and called equator.

So irrespective of all specific spheres (eg celestial, geographic earth or geographic mars) there are 2 angular coordinates that define an objects position.

One is Right Ascension (α) or Hour Angle and one is Declination (δ), defined for a celestial sphere.

The RA (α) is analogous to longitude or meridian for a geographic (planetary) sphere, denoted by, (λ).

The Declination (δ) is analogous to latitude for a geographic (planetary) sphere, denoted by, φ.